User:Shapeyness/sandbox/Explanatory indispensability argument
The explanatory indispensability argument[a] is an altered form of the Quine–Putnam indispensability argument in the philosophy of mathematics. It claims that we should believe in mathematical objects such as numbers because they are indispensable to scientific explanations of empirical phenomena. It differs from the original indispensability argument in its increased focus on specific explanations instead of whole theories and in its shift towards inference to the best explanation as a justification for belief in mathematical objects rather than confirmational holism.
Examples of specific explanations proposed as mathematical explanations in science include the prime-numbered life cycles of periodical cicadas, the hexagonal structure of bee honeycomb, and the Seven Bridges of Königsberg. Debate over these examples and others have generated an increased focus on the notion of mathematical explanation itself and what it would need to be like to support the explanatory indispensability argument. Objections to the argument include the idea that mathematics is only used as a representational device, even when featured in scientific explanations; that mathematics does not need to be true to be explanatory because it could be a useful fiction; and that the argument is circular and so begs the question.
Background
[edit]Philosophy of mathematics
[edit]Platonism vs nominalism
Epistemic access
An indispensability argument is an argument in which the conclusion is supported by the claim that its truth is indispensable or necessary for a certain purpose.[3]
Origin of the argument
[edit]The explanatory indispensability argument is an altered form of the Quine–Putnam indispensability argument[4] first raised by W. V. Quine and Hilary Putnam in the 1960s and 1970s.[5] The Quine–Putnam indispensability argument supports the conclusion that mathematical objects exist with the idea that mathematics is indispensable to our best scientific theories.[6] It relies on the view, called confirmational holism, that scientific theories are confirmed as wholes, and that the confirmations of science extend to the mathematics it makes use of.[7]
The reliance of the Quine–Putnam argument on confirmational holism is controversial, and it has faced influential challenges from Penelope Maddy and Elliott Sober.[8] The argument has also been criticized for failing to specify the way in which mathematics is indispensable to science; according to Joseph Melia, we only need to believe in mathematics if it is indispensable in the right way.[9] Specifically, it needs to be indispensable to scientific explanations for it to be as strongly justified as theoretical entities such as electrons.[10] This claim by Melia arose through a debate with Mark Colyvan in the early 2000s over the argument, with Colyvan claiming that mathematics enhances the explanatory power of science. Inspired by this debate, Alan Baker developed an explicitly explanatory form of the indispensability argument, which he termed the enhanced indispensability argument.[b][11] He was also motivated by the objections against confirmational holism; his formulation aimed to replace confirmational holism with an inference to the best explanation.[12]
Among Baker's influences was Hartry Field, who has been credited with being the first person to draw a connection between indispensability arguments and explanation.[13][c] Baker cited Field as originating an explanatory form of the argument,[15] although Sorin Bangu states that Field merely alluded to such an argument without fully developing it,[16] and Russell Marcus argues he was discussing explanation within the context of the original Quine–Putnam indispensability argument rather than suggesting a new explanatory indispensability argument.[17] According to Marcus, Colyvan's discussion of explanatory power was also initially restricted to its role within the Quine–Putnam indispensability argument. He credits Baker with originating the explanatory indispensability argument.[18] Others, such as Christopher Pincock, place the beginning of the argument's development with Colyvan while noting that Baker sharpened its explanatory focus.[19]
Lyon 2012 p. 572, maybe useful for characterising things too
[Busch & Sereni argue that it is fundamentally different to the QPIA argument and cannot be considered Quinean - maybe include? as an explanatory footnote after part about IBE?]
Overview
[edit]A standard formulation of the explanatory indispensability argument is given as follows:[20]
- We ought rationally to believe in the existence of any entity which plays an indispensable explanatory role in our best scientific theories.
- Mathematical objects play an indispensable explanatory role in science.
- Therefore, we ought rationally to believe in the existence of mathematical objects.
Individual examples in support of this argument come in the form of an inference to the best explanation, where the fact to be explained (explanandum) is the conclusion, and the things doing the explaining (explanans) are premises.[Bangu 2012 p.152]
The argument is premised on the idea that inference to the best explanation, which is often used to justify theoretical entities such as electrons, can provide a similar kind of support for mathematical objects.[21] It also requires that there are genuinely mathematical explanations in science. For explanations to be genuinely mathematical, it is not enough that they are expressed with the help of mathematics. Instead, the mathematics must be playing an essential part in the explanatory work.[22] Given the argument's reliance on the existence of such explanations, much of the discussion on it has focused on evaluating specific case studies to assess if they are genuinely mathematical explanations or not.[23]
Notes to self
Explain / discuss IBE (should distinction between epistemic / ontic explanation go here? Or in objections section?)
Maybe talk about target of argument (scientific realists) [Paseau & Baker, Baron 2020 p.19, Pincock 2011 p.211] and motivation from epistemological problem
Case studies
[edit]Periodical cicadas
[edit]
The most influential case study is the example of periodical cicadas provided by Baker.[24] Periodical cicadas are a type of insect that usually have life cycles of 13 or 17 years. It is hypothesized that this is an evolutionary advantage because 13 and 17 are prime numbers. Because prime numbers have no non-trivial factors, this means it is less likely that periodic predators and other competing species of cicada can synchronize with periodic cicadas' life cycles.[25] Baker argues that this is an explanation in which mathematics, specifically number theory, plays a key role in explaining an empirical phenomenon.[26]
A number of non-mathematical explanations have been proposed for the length of periodical cicadas' life cycles. For example, a prominent alternative explanation claims that prime-numbered life cycles could have emerged from non-prime life cycles due to developmental delays. This hypothesis is supported by the fact that there are many other species of cicada that have non-prime life cycles, and that developmental changes with 4-year periods have often been observed in periodical cicadas.[27] Some philosophers have also argued that the concept of primeness in the case study by Baker can be replaced with a non-numeric concept of "intersection-minimizing periods", although Baker has argued that this would reduce the generality and depth of the explanation.[28] Others, such as Chris Daly and Simon Langford, argue that using years as a unit of measurement rather than months or seasons is arbitrary; Baker and Colyvan argue that years are an appropriate unit of time for biological development and are the unit used by biologists.[29]
The case study has also been criticized for assuming that periodical cicadas have had predators with periodic life cycles in their evolutionary history.[30] Baker has responded to this worry by arguing that it would be impossible to provide direct evidence that periodical cicadas have had periodic predators because "periodicity is not something that can be gleaned from the fossil record".[31] However, he has attempted to make the claim more plausible by arguing that ecological constraints could have restricted the range of the cicadas' possible life cycles, lessening the requirements on periodic predators for the case study to remain mathematically sound.[32] This problem can also be avoided by focusing on other ways in which the prime life cycles could be explanatorily relevant, such as avoidance of competing species of cicada or periodic migration of predators.[33]
Bee honeycomb
[edit]Another prominent case study suggested by Aidan Lyon and Colyvan is the hexagonal structure of bee honeycomb. Lyon and Colyvan contend that the hexagonal structure of bee honeycomb can be explained by the mathematical proof of the honeycomb conjecture, which states that hexagons are the most efficient regular tiling of the plane. The explanation goes that there is an evolutionary pressure for honeybees to conserve wax in the construction of there combs, so the efficiency of the hexagonal grid explains why it is selected for.[34]
The explanation based on the honeycomb conjecture is potentially incomplete because the proof is a solution to a tiling problem in two dimensions, and disregards the 3D structure of comb cells.[35] Furthermore, many mathematicians do not see the proof of the honeycomb conjecture as an explanatory proof as it employs concepts outside of geometry to establish a geometrical result,[36] although Baker argues that the proof need not be explanatory for the theorem to feature in genuine explanations in science.[37] It is also controversial amongst philosophers whether the subject matter of geometry is purely mathematical, or whether it concerns physical space and structures, leading them to question if the explanation is truly mathematical.[38]
There are also non-mathematical explanations for the honeycomb case study. Darwin believed that the hexagonal shape of bee combs was the result of tightly packed spherical cells being pushed together and pressed into hexagons, with bees fixing breakages with flat surfaces of wax further contributing to a hexagonal shape.[39] More modern presentations hold that the shape of honeycomb is due to the flow of molten wax during the construction process.[40]
Others
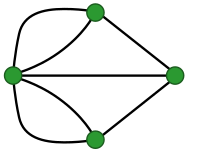
[edit]Another key example is the Seven Bridges of Königsberg, which concerns the impossibility of crossing each of the historical seven bridges in the Prussian city of Königsberg a single time in a continuous walk around the city.[d] The explanation was found by Leonhard Euler in 1735 when he considered whether such a journey was possible.[41] Euler's solution involved abstracting away from the concrete details of the problem to a mathematical representation in the form of a graph, with nodes representing landmasses and lines representing bridges.[42] He reasoned that for each landmass, unless it is a starting or ending point, there must be a path to both enter and exit it. Therefore, there must be at most two nodes in the graph with an uneven number of lines connected to them for such a journey to be possible. But this is not the case for the graph representing the seven bridges in Königsberg, so it is mathematically impossible to cross all seven without crossing over one of the bridges multiple times.[43]
The existence at any particular time of antipodal points on the Earth's surface with equal temperature and pressure has been cited as another example. According to Colyvan, this is explained by the Borsuk–Ulam theorem, which entails that for any physical property that varies continuously across the surface of a sphere, there are antipodal points on that sphere with equal values of that property.[44] In response to this example, Baker has argued that it is a prediction rather than an explanation because antipodal points with equal pressure and temperature have not already been measured.[45] Mary Leng also questions whether it is appropriate to model temperature or pressure as continuous functions across individual points on the Earth's surface.[46][e]
A key class of mathematical explanations is solutions to optimization problems, which includes the cicada and bee honeycomb case studies. In these cases, a certain feature is explained by showing that it is mathematically optimal.[48] Such explanations are important in evolutionary biology, as mathematical demonstrations of optimality may help to explain why a given trait has been selected for,[49] but also appear in other areas of science such as physics, engineering and economics.[50] Some examples from evolutionary biology are sunflowers' seeds being arranged in a spiral pattern because it produces the densest packing of seeds,[51] and marine predators engaging in Lévy walks because they minimize the average energy consumption required to find prey.[52][f]
A number of case studies draw from dynamical systems. Marc Lange, for example, argues that the fact that double pendulums always have four or more equilibrium configurations can be explained by the configuration space of the system forming the surface of a torus, which must have at least four stationary points.[54] Lyon and Colyvan point to the use of phase spaces and the Poincaré map to explain the behaviour of a Hénon–Heiles system, such as the stability of a star's orbit through a galaxy.[55] Other examples proposed by Colyvan include geometrical explanations for Lorentz contraction and gravitational lensing. Baker and Melia have objected to the geometrical aspects of these explanations, which could be interpreted physically instead of mathematically.[56]
Some examples are drawn from outside science. For example, widely discussed cases include the explanation for why 23 strawberries cannot be divided equally amongst three people,[57] why it is impossible to square the circle,[58] and why it is impossible to untie a trefoil knot.[59] However, it is unclear to what extent each of these cases are mathematical explanations of physical facts rather than either purely physical or purely mathematical explanations.[g]
Mathematical explanation
[edit]Whilst the initial focus of the argument lay in the evaluation of specific cases, disagreement about their status as genuine examples of mathematical explanation prompted a greater focus on providing a theory of mathematical explanation itself. A number of theories have arisen, some favouring the argument and others contradicting it, as well as a deeper consideration of what the explanatory indispensability argument requires from a theory of mathematical explanation to be successful. [cite all this]
General features
[edit]Mathematical explanations are non-causal explanations since their explanatory power does not result from uncovering the causal connection between events.[63] They are generally seen as being modally stronger than causal explanations or physical laws. For example, it would still be impossible to cross the seven bridges of Königsberg even if the laws of physics were different, implying that mathematical explanation involves a stronger notion of necessity than physical necessity.[64] A successful theory of mathematical explanation should be able to distinguish between genuinely explanatory uses of mathematics and uses that are merely representational.[65][h] And, for the explanatory indispensability argument to succeed, mathematical explanation must not be relative to the person or context, since this would make it impossible to determine whether a mathematical explanation was a genuine explanation or not.[67]
A distinction relevant to the argument is between epistemic and ontic explanation. Ontic explanation explains an event by uncovering the structure of the world; such explanations are generally committed to the existence of any entities that feature in them. Epistemic explanation, on the other hand, explains an event in the sense that it provides understanding or relates the event to something more familiar. Epistemic explanations do not necessarily commit us to the existence of anything, since even metaphors and analogies can provide understanding of a phenomenon.[68] Opponents of the explanatory indispensability argument tend to argue that all mathematical explanations are epistemic explanations, if there are any, while proponents of the argument claim that at least some mathematical explanations are ontic explanations.[69]
Theories of mathematical explanation
[edit]The philosophical study of mathematical explanations in science dates back to Aristotle, but within analytic philosophy, the first philosopher to deal with the issue was Mark Steiner, beginning in the 1970s.[70] According to Steiner, a mathematical explanation in science is genuinely mathematical if when the physical details are removed, a mathematical explanation of a mathematical fact remains. [cite this] Since then, there has been increasing attention on the question, and the explanatory indispensability argument has coincided with a greater emphasis on issues within the philosophy of mathematical practice more generally.[71] As a result, a number of competing theories of mathematical explanation have arisen, some favouring the argument and others contradicting it.[72]
Classic theories of explanation in the philosophy of science have focused on the role of causation and laws of nature in scientific explanations.[73] This focus cannot be directly transferred to mathematical explanations because mathematical explanations are modally stronger than causal laws.[74] However, the idea can be loosened to include mathematical dependence relations between mathematical objects and physical things.[75] Dependence relations are often analyzed in terms of counterfactuals, claims about what would have been the case if things were different in a particular way. For example, the bridges of Königsberg could have been crossed a single time each if they had a structure represented by a different mathematical graph, implying that there may be a dependence relation between the impossibility of crossing the seven bridges and their associated graph.[76] Other examples are more contentious since they use counterfactuals about impossible worlds, such as the claim that if 13 were not a prime number, then periodical cicadas would not have evolved with 13-year life cycles.[77][i]
Another law-based approach focuses on the modal constraints placed on a system by laws. According to Lange, for example, explanations based on physical laws have a certain level of modal strength which guarantees that what is being explained must have occurred. For example, the explanation for why ... is because the laws of nature guarantee this must be the case. Mathematical explanations are similar but provide stronger modal constraints than physical explanations. A similar approach... [program explanation, find a source to link (Lange?)]
Instead of broadening an account of causal explanation to cover non-causal explanations, some philosophers hold that causal and non-causal explanations are fundamentally different but equally genuine types of explanation.
Steiner vs Baker (Lyon, Mancosu, Tarziu b, Pincock 2023, see also 1, 2 )
Theories of mathematical explanation
Baron - heavy duty platonism, nomic theory, mapping account, entailment-based views, nomic-entailment, counterfactual dependence, pragmatic theories ('why' questions account), relevance logic
Lyon - program explanations (he introduced them in this paper, so maybe more of a primary source)
Mancosu et al. - Pythagoreanism vs Aristotelianism, see also section 1.2: nomic/counterfactual/counter-mathematical, program explanation, ontic structural realism, topological explanation
Pincock 2015 - section 4: program explanations, Lange, dependence relations
Pincock 2023 - Ch.2 Counterfactual accounts, Ch.3 Steiner and Lange, section 5.2 also discusses Pythagoreanism vs Aristotelianism
Saatsi - program explanations, counterfactual account, kairetic (i.e. difference-making) account
Vineberg - unification, difference making/counterfactual dependence, mathematical structuralism
Maybe useful sources: Baron 2016 (b), Lyon, Mancosu, Mancosu et al, Marcus ch.7, Paseau & Baker, Pincock sources, Saatsi 2016, Tarziu sources, Vineberg
Lange 2016/2021 may be useful (?)
Objections
[edit]The main response to the explanatory indispensability argument, adopted by philosophers such as Melia, Daly, Langford, and Saatsi, is to deny there are genuinely mathematical explanations of empirical phenomena, instead framing the role of mathematics as representational or indexical.[79] According to this response, if mathematics features in scientific explanations, its role is just to help pick out physical facts instead of contributing to the explanatory power of the explanation.[72] Saatsi, and others including Jonathan Tallant and Davide Rizza, have rephrased case studies such as the periodic cicada example to remove reference to mathematical entities in an attempt to provide the true non-mathematical versions of these explanations.[80] Defenders of the explanatory indispensability argument typically argue that the non-mathematical explanations provided are less general and modally weaker than mathematical explanations. They also argue that such explanations contradict scientific practice because scientists often accept the mathematical explanations as genuine scientific explanations.[81]
[ Other things that could be included: these paraphrases may not be nominalistically acceptable (Paseau & Baker), defenders of EIA need to show that there is a connection between modal strength and ontological commitment (Bueno & French), also that there is a connection between generality and the quality of the explanation (Falguera & Martínez-Vidal Ch. 3, p.42, Vineberg, p.238), weaseling (Bueno & French, p.165) ]
Others, particularly mathematical fictionalists like Mary Leng and Stephen Yablo, have accepted that mathematics plays a genuinely explanatory role in science but argue it can play this role even if mathematical objects do not exist.[72] They point to the use of idealizations like point masses that are used in scientific explanations but are not viewed as literally real.[82][j] Leng argues that the explanatory power of mathematics can be explained by structural similarities between mathematical theory (viewed fictionally) and features of the real world.[84] Yablo appeals to the expressive power of figurative language, claiming it shows that literally untrue statements can often convey more than literally true statements.[85] Colyvan has challenged these types of responses by arguing that fictional or metaphorical language cannot play a role in genuine explanations: "when some piece of language is delivering an explanation, either that piece of language must be interpreted literally or the non-literal reading of the language in question stands proxy for the real explanation."[86]
An objection advanced by Bangu states that the explanatory indispensability argument begs the question because it is circular. Bangu argues that examples like the periodic cicada case aim to explain statements that already contain mathematical content, namely the primeness of the cicadas' life cycles. But an inference to the best explanation assumes that the statement being explained is true, so inclusion of mathematical concepts such as primeness assume the truth of the mathematics in question.[87][k] Baker has responded to this objection by arguing that the statements being explained in ,such case studies can be reformulated to remove reference to mathematical entities, leaving mathematics indispensable only to the explanation itself and not the thing being explained.[89]
Notes on sources
[edit]- Baron 2016 (a) - implications of access problem for explanatory indispensability argument
- Baron 2016 (b) - different theories of mathematical explanation: heavy duty platonism, nomic theory of explanation, mapping account, entailment-based views, nomic-entailment, counterfactual dependence, pragmatic theories ('why' questions account), relevance logic
- still need to read Lange 2021
- Lyon - discussion of Steiner's view of mathematical explanation & Baker's criticisms + program explanations (§3) - objections from Colyvan and Daly & Langford are covered in §4
- Mancosu - Steiner's views on mathematical explanation + Baker's criticism (§5.1) - intra-mathematical explanation, e.g. explanatory vs non-explanatory proofs (§5.3)
- Mancosu et al. - Explanatory Indispensability Arguments section: Final two paragraphs talk about differing theories of mathematical explanation either supporting or contradicting EIA - probably need to check through the rest of the article to see if there is anything else useful
- Marcus Ch. 7 - §Two Concepts of Explanation & §Epistemic Explanation and the Explanatory Indispensability Argument cover different theories of explanation and epistemic vs ontic explanation
- Molinini (also discussed in Pataut paper in Synthese special issue) - discussion of Baker's idea that use of stronger mathematical apparatus can reduce nominalistic commitments, meaning mathematics contributes to nominalistic parsimony
- Synthese special issue - Baron and de Bianchi discuss indispensable use of idealizations in science, Molinini and Sereni discuss the problem of equivalent mathematical explanations, which is also discussed by Hunt, Hunt and Busch & Morrison discuss IBE and whether it supports mathematical explanations equally to other scientific explanations (parity premise), Panza & Sereni and Galinon (still need to read, very technical/complex papers), Liggins and Plebani discuss nominalists' possible use of grounding to undermine EIA
- Paseau & Baker - §5.4 The Audience for EIA - §6.3 restrictions to IBE, discusses epistemic explanation vs ontic explanation, eleatic arguments, "makes no difference" arguments - §7.4 discusses Hellman's modal structuralism, probably don't need to include here - everything else is pretty much covered already
- Pincock 2011 - Is the explanation mathematical? Is it the best explanation? Replacement test + Comparison test can answer these questions - Melia & indexing (already covered in this article) - ways mathematics can contribute to the explanatory power (all from 10.1) - IBE only works for mathematical claims if the mathematics is already justified (a similar idea is mentioned in Bangu at some point) - problem of weaker alternative mathematical explanations - restrictions on IBE (all from 10.2) - not much in 10.3
- Read Pincock 2015 & 2023
- Saatsi 2016 - different theories of explanation: programme explanations, counterfactual account, kairetic (i.e. difference-making) account
- Tarziu (a) - discussion of how to distinguish genuine mathematical explanations from merely mathematicised explanations, i.e how to tell if mathematics is explanatorily relevant - presents the importance view of explanatory relevance + different degrees of explanatory relevance - looks at Saatsi, Daly & Langford's criticisms of the cicada case study - probably not much useful left here for this article
- Tarziu (b) - connection between explanation and understanding (probably not too relevant for EIA) - discussion of Steiner's view of mathematical explanation & Baker's criticisms - mapping account - inferential conception
- Tarziu (c) - §5. Lange’s and Pincock’s accounts of mathematical explanation - explains their accounts, argues their piecemeal/case-driven approach is question-begging in the context of EIA because the cases chosen can always be questioned by nominalists - this discussion is then slightly widened in §6 - §7 is about possible ways of reliably identifying genuine scientific explanations (intuition, understanding, expert testimony)
- Vineberg - discussion of IBE and different principles that could underly it + what type of principle could be useful for EIA (both in terms of making the argument work and also in keeping it dialectically tenable) + possible analogy between causal and non-causal explanation (§Explanation and inference onwards) - discusses Jansson and Saatsi's arguments against Konigsberg bridges case study (§Mathematical explanation and difference makers)
- Wakil & Justus - claim that biological optimality examples make a fallacious jump from mathematics explaining the adaptiveness of a trait (A-question) to mathematics explaining the existence of that trait (E-question); they further claim that EIA requires mathematics to explain E-questions to work - probably not space for this idea, but could maybe be added in a note
- Wójtowicz - probably not much more useful here - interesting discussion (§4 onwards) on formalised, purely-syntactic mathematics required for QPIA (regimentation into formal language) vs informal, semantic proofs required by EIA that provide explanatory power, but unlikely to fit into this article - very brief mention of the question of whether EIA requires an explanatory proof, or whether a theorem itself can be explanatory (without needing an explanatory proof)
Notes
[edit]- ^ Also known as the enhanced indispensability argument[1] or explanationist indispensability argument[2]
- ^ See Baker (2005, 2009)
- ^ See Field 1989. Other important precursors to the argument are Mark Steiner (1978a, 1978b) and J. J. C. Smart (1990) for their work on mathematical explanation.[14]
- ^ Sometimes the additional requirement that the journey must begin and end at the same place is posed as part of the problem.
- ^ According to Jha et al., the continuity of temperature is "a contingent causal phenomenon that depends on various factors" and "[t]emperature discontinuities across interfaces [have] been widely confirmed both on theoretical and experimental grounds".[47]
- ^ Related to optimization explanations are explanations regarding minimization processes, such as the explanation of the shape of soap films from Plateau's laws which show that they minimize surface area.[53]
- ^ Attributed to multiple sources: strawberry case study,[60] squaring the circle case study,[61] trefoil knot case study.[62]
- ^ A related condition is that a theory of mathematical explanation should respect the distinction between mathematics explaining a fact and mathematics providing evidence or justification for believing in that fact.[66]
- ^ Such an approach arguably over-generates mathematical explanations. For example, a train travelling 10 metres per second reaches a station 10 metres away in 1 second because 10/10 = 1, but this would not be the case if 10/10 did not equal 1. But intuitively this is an explanation in which mathematics is only playing a representational role; the true explanation for why the train takes 1 second to reach the station concerns the physical distance to the station and the physical speed of the train.[78]
- ^ Some idealizations can arguably be rephrased as true claims about limiting cases of real phenomena, so do not support the fictionalist argument. For example, scientific explanations featuring frictionless slopes can be viewed as making true claims about slopes as friction is reduced to zero. However, other idealizations are false even in the limiting case – fluid dynamics, for instance, models fluids as continuous substances even though all actual substances are composed of discrete atoms.[83]
- ^ A similar argument can be found from Steiner, who in 1978 claimed that "no explanatory argument can establish the existence of mathematical entities". According to Steiner, any description of the world necessarily presupposes the existence of mathematics, so it is impossible to compare mathematical explanations and non-mathematical explanations.[88]
References
[edit]Citations
[edit]- ^ Baker 2016a, p. 225; Pincock 2023, p. 61.
- ^ Hunt 2016, pp. 452–453; Bangu 2012, pp. 150–151, see also note 8 on p. 226.
- ^ Colyvan 2023, Introduction.
- ^ Drekalović & Žarnić 2018, p. 121; Molinini 2016, p. 404; Saatsi 2016, p. 1046.
- ^ Molinini, Pataut & Sereni 2016, p. 318.
- ^ Colyvan 2023, Introduction and §1.
- ^ Colyvan 2023, §3.
- ^ Colyvan 2023, §§4–5; Boyce 2021, p. 584.
- ^ Târziu 2018a, p. 396; Bangu 2012, pp. 147–148; Baron 2014, p. 460.
- ^ Heylen & Tump 2021, p. 3034; Lyon 2012, p. 572.
- ^ Lyon 2012, p. 572; Pincock 2023, p. 61; Mancosu, Poggiolesi & Pincock 2023, §1.4.
- ^ Târziu 2018a, pp. 396–397.
- ^ Molinini, Pataut & Sereni 2016, p. 320; Bangu 2012, p. 150.
- ^ Colyvan 2023, Bibliography; Colyvan & Resnik 2023.
- ^ Marcus 2015, p. 127.
- ^ Bangu 2012, p. 150.
- ^ Marcus 2015, pp. 127–130.
- ^ Marcus 2015, p. 130.
- ^ Pincock 2012, p. 203; Pincock 2023, p. 61.
- ^ Paseau & Baker 2023, p. 34.
- ^ Busch & Morrison 2016, p. 439.
- ^ Wójtowicz 2020, p. 184; Busch & Morrison 2016, p. 438; Vineberg 2018, p. 237.
- ^ Bangu 2012, p. 152; Paseau & Baker 2023, p. 35.
- ^ Molinini, Pataut & Sereni 2016, p. 320; Baker 2005.
- ^ Barrantes 2019, p. 250; Leng 2005, pp. 184–185.
- ^ Colyvan 2023, §5; Paseau & Baker 2023, pp. 35–36.
- ^ Wakil & Justus 2017, pp. 918–919.
- ^ Barrantes 2019, pp. 251–253; McCullough-Benner 2022, pp. 754–758; Saatsi 2011, p. 150; Martínez-Vidal & Rivas-de-Castro 2020, pp. 39–40.
- ^ Cellucci 2017, p. 329.
- ^ Dieveney 2021, p. 60; Drekalović 2019, p. 34.
- ^ Dieveney 2021, p. 60.
- ^ Dieveney 2021, p. 61.
- ^ Dieveney 2021, p. 72.
- ^ Baron 2014, pp. 461–462; Räz 2013, pp. 351–352; Lyon & Colyvan 2008.
- ^ Wakil & Justus 2017, p. 923; Cellucci 2017, p. 22; Räz 2013.
- ^ Baker 2015, pp. 237–239.
- ^ Lyon 2012, p. 564; Pincock 2023, p. 47.
- ^ Baron 2014, p. 462; Saatsi 2011, p. 148.
- ^ Wakil & Justus 2017, p. 921.
- ^ Wakil & Justus 2017, p. 922; Cellucci 2017, p. 22.
- ^ Lange 2013, pp. 488–489; Räz 2018, pp. 331–332; Pincock 2007.
- ^ Drekalović 2019, pp. 25–26; Vineberg 2018, p. 240.
- ^ Lange 2013, p. 489; Pantsar 2021, pp. 2595–2596; Vineberg 2018, p. 240.
- ^ Leng 2005, p. 181; Târziu 2018b, p. 93; Colyvan 2001, p. 49.
- ^ Marcus 2015, p. 131; Târziu 2018b, p. 93.
- ^ Marcus 2015, p. 131; Leng 2005, pp. 181–182.
- ^ Jha et al. 2024, p. 8.
- ^ Baker 2015, p. 241.
- ^ Baron 2014, p. 470.
- ^ Baker 2016b, p. 335; Mancosu, Poggiolesi & Pincock 2023, §1.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1; Lyon 2012, pp. 561–562.
- ^ Bangu 2018, p. 226; Baron 2014, pp. 464–465.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1.
- ^ Pincock 2023, pp. 48–49; Jha et al. 2022; Lange 2013.
- ^ Saatsi 2017, pp. 894–895; Friend & Molinini 2016, pp. 188–189; Lyon & Colyvan 2008.
- ^ Marcus 2015, pp. 130–131; Saatsi 2007, p. 30; Sereni 2016, p. 426; Colyvan 2001, §3.3.
- ^ Baker 2021b, pp. 2–4; Bueno & French 2018, pp. 163–164; Lange 2013.
- ^ Leng 2005, pp. 182–184; Colyvan 2007.
- ^ Târziu 2018c, p. 474; Jha et al. 2024, pp. 16–17; Lange 2013.
- ^ Baker 2021b, pp. 2–4; Bueno & French 2018, pp. 163–164.
- ^ Leng 2005, pp. 182–184.
- ^ Târziu 2018c, p. 474; Jha et al. 2024, pp. 16–17.
- ^ Lange 2013, p. 495.
- ^ Baron 2016, pp. 462–463; Lange 2013, p. 491.
- ^ Baron 2016, pp. 459–460; Vineberg 2018, p. 237.
- ^ Pincock 2023, p. 3.
- ^ Baron 2016, p. 459–460.
- ^ Marcus 2015, pp. 134–138; Saatsi 2016, pp. 1052–1053.
- ^ Paseau & Baker 2023, p. 43.
- ^ Mancosu 2008, §5.1; Molinini, Pataut & Sereni 2016, p. 322.
- ^ Paseau & Baker 2023, p. 52; Molinini, Pataut & Sereni 2016, p. 323.
- ^ a b c Mancosu, Poggiolesi & Pincock 2023, §1.4.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1.2.
- ^ Baron 2016, p. 462.
- ^ Pincock 2015, p. 869; Mancosu, Poggiolesi & Pincock 2023, §1.2; Saatsi 2016, p. 1060.
- ^ Pincock 2023, p. 20.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1.2; Baron 2016, p. 468.
- ^ Baron 2016, pp. 468–469; Mancosu, Poggiolesi & Pincock 2023, §1.2.
- ^ Molinini 2016, p. 405.
- ^ Paseau & Baker 2023, pp. 47–51.
- ^ Paseau & Baker 2023, p. 49; Bueno & French 2018, p. 162.
- ^ Paseau & Baker 2023, pp. 39–40.
- ^ Paseau & Baker 2023, p. 40.
- ^ Pincock 2020, p. 46; Mancosu, Poggiolesi & Pincock 2023, §1.4.
- ^ Colyvan 2012, §4.3; Liggins 2024, §3.5.5.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1.4; Paseau & Baker 2023, pp. 41–42.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1.4; Baker 2021a, p. 157; Heylen & Tump 2021, pp. 3055–3056.
- ^ Mancosu, Poggiolesi & Pincock 2023, §1.4; Mancosu 2008, p. 135; Steiner 1978b, pp. 19–20.
- ^ Heylen & Tump 2021, p. 3036; Baron 2020, pp. 20–21.
Sources
[edit]- Baker, Alan (2005). "Are There Genuine Mathematical Explanations of Physical Phenomena?". Mind. 114 (454): 223–238. doi:10.1093/mind/fzi223. ISSN 0026-4423 – via ResearchGate.
- Baker, Alan (2009). "Mathematical Explanation in Science". The British Journal for the Philosophy of Science. 60 (3): 611–633. doi:10.1093/bjps/axp025. ISSN 0007-0882 – via ResearchGate.
- Baker, Alan (2015). "Mathematical Explanation in Biology". In Braillard, Pierre-Alain; Malaterre, Christophe (eds.). Explanation in Biology: An Enquiry into the Diversity of Explanatory Patterns in the Life Sciences. Springer Nature. pp. 229–247. ISBN 978-94-017-9821-1 – via Swarthmore College.
- Baker, Alan (2016a). "Non-Optional Projects: Mathematical and Ethical". In Leibowitz, Uri D.; Sinclair, Neil (eds.). Explanation in Ethics and Mathematics: Debunking and Dispensability. Oxford University Press. pp. 220–235. ISBN 978-0-19-877859-2 – via Swarthmore College.
- Baker, Alan (2016b). "Parsimony and Inference to the Best Mathematical Explanation". Synthese. 193 (2): 333–350. doi:10.1007/s11229-015-0723-3. ISSN 0039-7857 – via Swarthmore College.
- Baker, Alan (2021a). "Circularity, Indispensability, and Mathematical Explanation in Science". Studies in History and Philosophy of Science. 88: 156–163. doi:10.1016/j.shpsa.2021.05.017. ISSN 0039-3681.
- Baker, Alan (2021b). "Bipedal Gait Costs: A New Case Study of Mathematical Explanation in Science". European Journal for Philosophy of Science. 11 (3). doi:10.1007/s13194-021-00411-3. ISSN 1879-4912.
- Bangu, Sorin (2012). The Applicability of Mathematics in Science: Indispensability and Ontology. New Directions in the Philosophy of Science. Palgrave Macmillan. ISBN 978-0-230-28520-0.
- Bangu, Sorin (2018). "Indispensability, Causation and Explanation". Theoria. 33 (2): 219–232. doi:10.1387/theoria.17619. ISSN 2171-679X.
- Baron, Sam (2014). "Optimisation and Mathematical Explanation: Doing the Lévy Walk". Synthese. 191 (3): 459–479. doi:10.1007/s11229-013-0284-2. ISSN 0039-7857.
- Baron, Sam (2016). "Explaining Mathematical Explanation". The Philosophical Quarterly. 66 (264): 458–480. doi:10.1093/pq/pqv123. ISSN 0031-8094.
- Baron, Sam (2020). "Purely Physical Explananda: Bistability in Perception". In Falguera, José L.; Martínez-Vidal, Concha (eds.). Abstract Objects: For and Against. Springer Nature. pp. 17–34. ISBN 978-3-030-38244-5.
- Barrantes, Manuel (2019). "Optimal Representations and the Enhanced Indispensability Argument". Synthese. 196 (1): 247–263. doi:10.1007/s11229-017-1470-4. ISSN 0039-7857 – via PhilPapers.
- Boyce, Kenneth (2021). "Why Inference to the Best Explanation Doesn't Secure Empirical Grounds for Mathematical Platonism". Synthese. 198 (1): 583–595. doi:10.1007/s11229-018-02043-2. ISSN 0039-7857 – via PhilPapers.
- Bueno, Otávio; French, Steven (2018). "Explaining with Mathematics? From Cicadas to Symmetry". Applying Mathematics: Immersion, Inference, Interpretation. Oxford University Press. pp. 151–182. ISBN 978-0-19-881504-4.
- Busch, Jacob; Morrison, Joe (2016). "Should Scientific Realists Be Platonists?". Synthese. 193 (2): 435–449. doi:10.1007/s11229-015-0676-6. ISSN 0039-7857 – via Queen's University Belfast.
- Cellucci, Carlo (2017). "Mathematical Explanations". Rethinking Knowledge: The Heuristic View. European Studies in Philosophy of Science. Vol. 4. Springer. pp. 315–334. ISBN 978-3-319-53237-0.
- Colyvan, Mark (2001). The Indispensability of Mathematics. Oxford University Press. ISBN 978-0-19-516661-3.
- Colyvan, Mark (2007). "Mathematical Recreation versus Mathematical Knowledge". In Leng, Mary; Paseau, Alexander C.; Potter, Michael (eds.). Mathematical Knowledge. Oxford University Press. pp. 109–122. ISBN 978-0-19-922824-9 – via PhilPapers.
- Colyvan, Mark (2012). An Introduction to the Philosophy of Mathematics. Cambridge University Press. ISBN 978-0-521-82602-0.
- Colyvan, Mark (2023). "Indispensability Arguments in the Philosophy of Mathematics". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Spring 2023 ed.). Metaphysics Research Lab, Stanford University. ISSN 1095-5054.
- Colyvan, Mark; Resnik, Michael (2023). "Explanation and Realism: Interwoven Themes in the Philosophy of Mathematics". In Posy, Carl; Ben-Menahem, Yemima (eds.). Mathematical Knowledge, Objects and Applications: Essays in Memory of Mark Steiner. Springer. pp. 41–58. ISBN 978-3-031-21654-1.
- Dieveney, Patrick (2021). "Scientific Explanation, Unifying Mathematics, and Indispensability Arguments (A New Cicada MES)". Synthese. 198 (1): 57–77. doi:10.1007/s11229-018-01979-9. ISSN 0039-7857.
- Drekalović, Vladimir (2019). "Mathematical Explanation as Part of an (Im)perfect Scientific Explanation: An Analysis of Two Examples". Filozofia Nauki. 27 (4): 23–41. doi:10.14394/filnau.2019.0024.
- Drekalović, Vladimir; Žarnić, Berislav (2018). "Which Mathematical Objects are Referred to by the Enhanced Indispensability Argument?". Journal for General Philosophy of Science. 49 (1): 121–126. doi:10.1007/s10838-017-9381-0. ISSN 0925-4560.
- Field, Hartry (1989). "Indispensability Arguments and Inference to the Best Explanation". Realism, Mathematics, and Modality. Wiley-Blackwell. pp. 14–20. ISBN 0-631-16303-4.
- Friend, Michèle; Molinini, Daniele (2016). "Using Mathematics to Explain a Scientific Theory". Philosophia Mathematica. 24 (2): 185–213. doi:10.1093/philmat/nkv022. ISSN 0031-8019.
- Heylen, Jan; Tump, Lars Arthur (2021). "The Enhanced Indispensability Argument, the Circularity Problem, and the Interpretability Strategy". Synthese. 198 (4): 3033–3045. doi:10.1007/s11229-019-02263-0. ISSN 0039-7857 – via PhilPapers.
- Hunt, Josh (2016). "Indispensability and the Problem of Compatible Explanations: A Reply to 'Should Scientific Realists Be Platonists?'". Synthese. 193 (2): 451–467. doi:10.1007/s11229-015-0667-7. ISSN 0039-7857.
- Jha, Aditya; Campbell, Douglas; Montelle, Clemency; Wilson, Phillip L. (2022). "Not So Distinctively Mathematical Explanations: Topology and Dynamical Systems". Synthese. 200 (3). doi:10.1007/s11229-022-03697-9. ISSN 1573-0964 – via PhilPapers.
- Jha, Aditya; Campbell, Douglas; Montelle, Clemency; Wilson, Phillip L. (2024). "Are Mathematical Explanations Causal Explanations in Disguise?". Philosophy of Science: 1–19. doi:10.1017/psa.2024.8. ISSN 0031-8248 – via PhilPapers.
- Lange, Marc (2013). "What Makes a Scientific Explanation Distinctively Mathematical?". The British Journal for the Philosophy of Science. 64 (3): 485–511. doi:10.1093/bjps/axs012. ISSN 0007-0882.
- Leng, Mary (2005). "Mathematical Explanation". In Cellucci, Carlo; Gillies, Donald A. (eds.). Mathematical Reasoning and Heuristics. King's College Publications. pp. 167–189. ISBN 1-904987-07-9.
- Liggins, David (2024). Abstract Objects. Cambridge Elements in Metaphysics. Cambridge University Press. ISBN 978-1-009-24140-3.
- Lyon, Aidan (2012). "Mathematical Explanations Of Empirical Facts, And Mathematical Realism". Australasian Journal of Philosophy. 90 (3): 559–578. doi:10.1080/00048402.2011.596216. ISSN 0004-8402.
- Lyon, Aidan; Colyvan, Mark (2008). "The Explanatory Power of Phase Spaces". Philosophia Mathematica. 16 (2): 227–243. doi:10.1093/philmat/nkm025. ISSN 0031-8019 – via PhilPapers.
- Mancosu, Paolo (2008). "Mathematical Explanation: Why it Matters". In Mancosu, Paolo (ed.). The Philosophy of Mathematical Practice. Oxford University Press. pp. 134–150. ISBN 978-0-1917-1196-1.
- Mancosu, Paolo; Poggiolesi, Francesca; Pincock, Christopher (2023). "Mathematical Explanation". In Zalta, Edward N. (ed.). The Stanford Encyclopedia of Philosophy (Fall 2023 ed.). Metaphysics Research Lab, Stanford University. ISSN 1095-5054.
- Marcus, Russell (n.d.). "The Indispensability Argument in the Philosophy of Mathematics". Internet Encyclopedia of Philosophy. ISSN 2161-0002. Archived from the original on July 25, 2023. Retrieved October 6, 2023.
- Marcus, Russell (2015). Autonomy Platonism and the Indispensability Argument. Lexington Books. ISBN 978-0-7391-7313-8.
- Martínez-Vidal, Concha; Rivas-de-Castro, Navia (2020). "Description, Explanation and Ontological Committment". In Falguera, José L.; Martínez-Vidal, Concha (eds.). Abstract Objects: For and Against. Springer Nature. pp. 35–57. ISBN 978-3-030-38241-4.
- McCullough-Benner, Colin (2022). "The Metarepresentational Role of Mathematics in Scientific Explanations". Philosophy of Science. 89 (4): 742–760. doi:10.1017/psa.2021.46. ISSN 0031-8248 – via White Rose Research Online.
- Molinini, Daniele (2016). "Evidence, Explanation and Enhanced Indispensability". Synthese. 193 (2): 403–422. doi:10.1007/s11229-014-0494-2. ISSN 0039-7857.
- Molinini, Daniele; Pataut, Fabrice; Sereni, Andrea (2016). "Indispensability and Explanation: An Overview and Introduction". Synthese. 193 (2): 317–332. doi:10.1007/s11229-015-0998-4. ISSN 0039-7857.
- Pantsar, Markus (2021). "Mathematical Explanations and Mathematical Applications". In Sriraman, Bharath (ed.). Handbook of the Mathematics of the Arts and Sciences. Springer Nature. pp. 2587–2602. ISBN 978-3-319-57071-6.
- Paseau, Alexander C.; Baker, Alan (2023). Indispensability. Cambridge Elements in the Philosophy of Mathematics. Cambridge University Press. ISBN 978-1-009-09685-0.
- Pincock, Christopher (2007). "A Role for Mathematics in the Physical Sciences". Noûs. 41 (2): 253–275. doi:10.1111/j.1468-0068.2007.00646.x. ISSN 0029-4624.
- Pincock, Christopher (2012). Mathematics and Scientific Representation. Oxford University Press. ISBN 978-0-19-975710-7.
- Pincock, Christopher (2015). "Abstract Explanations in Science". The British Journal for the Philosophy of Science. 66 (4): 857–882. doi:10.1093/bjps/axu016. ISSN 0007-0882.
- Pincock, Christopher (2020). "Mathematical Explanation Requires Mathematical Truth". In Dasgupta, Shamik; Dotan, Ravit; Weslake, Brad (eds.). Current Controversies in Philosophy of Science. Routledge. pp. 39–50. ISBN 978-1-138-82577-2.
- Pincock, Christopher (2023). Mathematics and Explanation. Cambridge Elements in the Philosophy of Mathematics. Cambridge University Press. ISBN 978-1-009-03915-4.
- Räz, Tim (2013). "On the Application of the Honeycomb Conjecture to the Bee's Honeycomb" (PDF). Philosophia Mathematica. 21 (3): 351–360. doi:10.1093/phimat/nkt022. ISSN 0031-8019 – via PhilSci-Archive.
- Räz, Tim (2018). "Euler's Königsberg: The Explanatory Power of Mathematics" (PDF). European Journal for Philosophy of Science. 8 (3): 331–346. doi:10.1007/s13194-017-0189-x. ISSN 1879-4912 – via PhilSci-Archive.
- Saatsi, Juha (2007). "Living in Harmony: Nominalism and the Explanationist Argument for Realism". International Studies in the Philosophy of Science. 21 (1): 19–33. doi:10.1080/02698590701305743. ISSN 0269-8595.
- Saatsi, Juha (2011). "The Enhanced Indispensability Argument: Representational versus Explanatory Role of Mathematics in Science". The British Journal for the Philosophy of Science. 62 (1): 143–154. doi:10.1093/bjps/axq029. ISSN 0007-0882.
- Saatsi, Juha (2016). "On the 'Indispensable Explanatory Role' of Mathematics". Mind. 125 (500): 1045–1070. doi:10.1093/mind/fzv175. ISSN 0026-4423 – via White Rose Research Online.
- Saatsi, Juha (2017). "Dynamical Systems Theory and Explanatory Indispensability". Philosophy of Science. 84 (5): 892–904. doi:10.1086/693965. ISSN 0031-8248 – via White Rose Research Online.
- Sereni, Andrea (2016). "Equivalent Explanations and Mathematical Realism. Reply to 'Evidence, Explanation, and Enhanced Indispensability'". Synthese. 193 (2): 423–434. doi:10.1007/s11229-014-0491-5. ISSN 0039-7857.
- Smart, J. J. C. (1990). "Explanation—Opening Address". In Knowles, Dudley (ed.). Explanation and Its Limits. Cambridge University Press. pp. 1–19. ISBN 978-0-521-39598-4.
- Steiner, Mark (1978a). "Mathematical Explanation". Philosophical Studies. 34 (2): 135–151. doi:10.1007/bf00354494. ISSN 0031-8116.
- Steiner, Mark (1978b). "Mathematics, Explanation, and Scientific Knowledge". Noûs. 12 (1): 17. doi:10.2307/2214652. ISSN 0029-4624.
- Târziu, Gabriel (2018a). "Importance and Explanatory Relevance: The Case of Mathematical Explanations". Journal for General Philosophy of Science. 49 (3): 393–412. doi:10.1007/s10838-018-9424-1. ISSN 0925-4560 – via PhilPapers.
- Târziu, Gabriel (2018b). "Can We Have Mathematical Understanding of Physical Phenomena?". Theoria. 33 (1): 91–109. doi:10.1387/theoria.18108. ISSN 0495-4548. JSTOR 26355571.
- Târziu, Gabriel (2018c). "Mathematical Explanations and the Piecemeal Approach to Thinking About Explanation". Logique et Analyse. 244 (2018): 457–487. doi:10.2143/LEA.244.0.3285351. ISSN 2295-5836. JSTOR 26767893 – via PhilPapers.
- Vineberg, Susan (2018). "Mathematical Explanation and Indispensability". Theoria. 33 (2): 233. doi:10.1387/theoria.17615. ISSN 2171-679X.
- Wakil, Samantha; Justus, James (2017). "Mathematical Explanation and the Biological Optimality Fallacy". Philosophy of Science. 84 (5): 916–930. doi:10.1086/694154. ISSN 0031-8248 – via ResearchGate.
- Wójtowicz, Krzysztof (2020). "The Status of Mathematical Proofs and the Enhanced Indispensability Argument". In Będkowski, Marcin; Brożek, Anna; Chybińska, Alicja; Ivanyk, Stepan; Traczykowski, Dominik (eds.). Formal and Informal Methods in Philosophy. Brill. pp. 180–194. ISBN 978-90-04-42049-6.
Further reading
[edit]- Indispensability Arguments in Mathematics, Explanation in Mathematics, and Mathematical Explanation at PhilPapers
- Bangu, Sorin (March 27, 2014). "Indispensability of Mathematics". Oxford Bibliographies Online. Retrieved October 8, 2023.
- Mancosu, Paolo; Pincock, Christopher (August 29, 2012). "Mathematical Explanation". Oxford Bibliographies Online. Retrieved July 7, 2024.