Black hole

For other uses, see Black hole (disambiguation).

A black hole is an object predicted by general relativity with a gravitational field so strong that nothing can escape it — not even light.

A black hole is defined to be a region of space-time where escape to the outside universe is impossible. The boundary of this region is a surface called the event horizon. This surface is not a physically tangible one, but merely a figurative concept of an imaginary boundary. Nothing can move from inside the event horizon to the outside, even briefly.

The existence of black holes in the universe is well supported by astronomical observation, particularly from studying X-ray emission from X-ray binaries and active galactic nuclei. It has also been hypothesized that black holes radiate energy due to quantum mechanical effects known as Hawking radiation.

History

The concept of a body so massive that even light could not escape was put forward by the English geologist John Michell in a 1784 paper sent to Henry Cavendish and published by the Royal Society. At that time, the Newtonian theory of gravity and the concept of escape velocity were well known. Michell computed that a body with 500 times the radius of the Sun and of the same density would have, at its surface, an escape velocity equal to the speed of light, and therefore would be invisible. In his words:

If the semi-diameter of a sphere of the same density as the Sun were to exceed that of the Sun in the proportion of 500 to 1, a body falling from an infinite height towards it would have acquired at its surface greater velocity than that of light, and consequently supposing light to be attracted by the same force in proportion to its vis inertiae (inertial mass), with other bodies, all light emitted from such a body would be made to return towards it by its own proper gravity.

Michell considered the possibility that many such objects that cannot be seen might be present in the cosmos.

In 1796, the French mathematician Pierre-Simon Laplace promoted the same idea in the first and second edition of his book Exposition du système du Monde. It disappeared in later editions. The whole idea gained little attention in the nineteenth century, since light was thought to be a massless wave, not influenced by gravity.

In 1915, Albert Einstein developed the theory of gravity called General Relativity. Earlier he had shown that gravity does influence light. A few months later, Karl Schwarzschild gave the solution for the gravitational field of a point mass and a spherical mass, showing that something we now call a black hole could theoretically exist. The Schwarzschild radius is now known to be the radius of the event horizon of a non-rotating black hole, but this was not well understood at that time. Schwarzschild himself thought it was not physical. In a remarkable coincidence, the name Schwarzschild actually translates into black shield. In another coincidence, only a few months after Schwarzschild, a student of Lorentz, Johannes Droste, independently gave the same solution for the point mass as Schwarzschild had and wrote even more extensively about its properties.

In 1930, Subrahmanyan Chandrasekhar argued that special relativity demonstrated that a non-radiating body above 1.44 solar masses, now known as the Chandrasekhar limit, would collapse since there was nothing known at that time that could stop it from doing so. His arguments were opposed by Arthur Eddington, who believed that something would inevitably stop the collapse. Both were correct, since a white dwarf more massive than the Chandrasekhar limit will collapse into a neutron star. However, a neutron star above about three solar masses (the Tolman-Oppenheimer-Volkoff limit) will itself become unstable against collapse due to similar physics.

In 1939, Robert Oppenheimer and H. Snyder predicted that massive stars could undergo a dramatic gravitational collapse. Black holes could, in principle, be formed in nature. Such objects for a while were called frozen stars since the collapse would be observed to rapidly slow down and become heavily redshifted near the Schwarzschild radius. The mathematics showed that an outside observer would see the surface of the star frozen in time at the instant where it crosses that radius. However, these hypothetical objects were not the topic of much interest until the late 1960s. Most physicists believed that they were a peculiar feature of the highly symmetric solution found by Schwarzschild, and that objects collapsing in nature would not form black holes.

Interest in black holes was rekindled in 1967 because of theoretical and experimental progress. In 1970, Stephen Hawking and Roger Penrose proved that black holes are a generic feature in Einstein's theory of gravity, and cannot be avoided in some collapsing objects. Interest was renewed in the astronomical community with the discovery of pulsars. Shortly thereafter, the use of the expression "black hole" was coined by theoretical physicist John Wheeler, being first used in his public lecture Our Universe: the Known and Unknown on 29 December 1967. The older Newtonian objects of Michell and Laplace are often referred to as "dark stars" to distinguish them from the "black holes" of general relativity.

Evidence

A (simulated) Black Hole of ten solar masses as seen from a distance of 600 km with the Milky Way in the background (horizontal camera opening angle: 90°).

]

Observation

Formation of extragalactic jets from a black hole's accretion disk

In theory, no object beyond the event horizon of a black hole can ever escape, including light. However, black holes can be inductively detected from observation of phenomena near them, such as gravitational lensing, galactic jets, and stars that appear to be in orbit around space where there is no visible matter.

The most conspicuous effects are believed to come from matter accreting onto a black hole, which is predicted to collect into an extremely hot and fast-spinning accretion disk. The internal viscosity of the disk causes it to become extremely hot, and emit large amounts of X-ray and ultraviolet radiation. This process is extremely efficient and can convert about 10% of the rest mass energy of an object into radiation, as opposed to nuclear fusion which can only convert a few percent of the mass to energy. Other observed effects are narrow jets of particles at relativistic speeds heading along the disk's axis.

However, accretion disks, jets, and orbiting objects are found not only around black holes, but also around other objects such as neutron stars and white dwarfs; and the dynamics of bodies near these non-black hole attractors is largely similar to that of bodies around black holes. It is currently a very complex and active field of research involving magnetic fields and plasma physics to disentangle what is going on. Hence, for the most part, observations of accretion disks and orbital motions merely indicate that there is a compact object of a certain mass, and says very little about the nature of that object. The identification of an object as a black hole requires the further assumption that no other object (or bound system of objects) could be so massive and compact. Most astrophysicists accept that this is the case, since according to general relativity, any concentration of matter of sufficient density must necessarily collapse into a black hole.

One important observable difference between black holes and other compact massive objects is that any infalling matter will eventually collide with the latter at relativistic speeds, leading to emission as the kinetic energy of the matter is thermalised. In addition thermonuclear "burning" may occur on the surface as material builds up. These processes produce irregular intense flares of X-rays and other hard radiation. Thus the lack of such flare-ups around a compact concentration of mass is taken as evidence that the object is a black hole, with no surface onto which matter can collect.

Suspected black holes

File:Cygnus-X-1.jpg

Location of the X-ray source Cygnus X-1 which is widely accepted to be a 10 solar mass black hole orbiting a blue giant star

An artist depiction of two black holes merging.

There is now a great deal of indirect astronomical observational evidence for black holes in two mass ranges:

• stellar mass black holes with masses of a typical star (4–15 times the mass of our Sun), and
• supermassive black holes with masses ranging from on the order of $10^{5}$ to $10^{10}$ solar masses.

Additionally, there is some evidence for intermediate-mass black holes (IMBHs), those with masses of a few hundred to a few thousand times that of the Sun. These black holes may be responsible for the emission from ultraluminous X-ray sources (ULXs).

Candidates for stellar-mass black holes were identified mainly by the presence of accretion disks of the right size and speed, without the irregular flare-ups that are expected from disks around other compact objects. Stellar-mass black holes may be involved in gamma ray bursts (GRBs); short duration GRBs are believed to be caused by colliding neutron stars, which form a black hole on merging. Observations of long GRBs in association with supernovae suggest that long GRBs are caused by collapsars; a massive star whose core collapses to form a black hole, drawing in the surrounding material. Therefore, a GRB could possibly signal the birth of a new black hole, aiding efforts to search for them.

Candidates for more massive black holes were first provided by the active galactic nuclei and quasars, discovered by radioastronomers in the 1960s. The efficient conversion of mass into energy by friction in the accretion disk of a black hole seems to be the only explanation for the copious amounts of energy generated by such objects. Indeed the introduction of this theory in the 1970s removed a major objection to the belief that quasars were distant galaxies — namely, that no physical mechanism could generate that much energy.

From observations in the 1980s of motions of stars around the galactic centre, it is now believed that such supermassive black holes exist in the centre of most galaxies, including our own Milky Way. Sagittarius A* is now generally agreed to be the location of a supermassive black hole at the centre of the Milky Way galaxy. The orbits of stars within a few AU of Sagittarius A* rule out any object other than a black hole at the centre of the Milky Way assuming the current standard laws of physics are correct.

The jet emitted by the galaxy M87 in this image is thought to be caused by a supermassive black hole at the galaxy's centre

The current picture is that all galaxies may have a supermassive black hole in their centre, and that this black hole accretes gas and dust in the middle of the galaxies generating huge amounts of radiation — until all the nearby mass has been swallowed and the process shuts off. This picture may also explain why there are no nearby quasars.

Although the details are still not clear, it seems that the growth of the black hole is intimately related to the growth of the spheroidal component — an elliptical galaxy, or the bulge of a spiral galaxy — in which it lives.

In 2002, the Hubble Telescope identified evidence indicating that intermediate size black holes exist in globular clusters named M15 and G1. The evidence for the black holes stemmed from the orbital velocity of the stars in the globular clusters; however, a group of neutron stars could cause similar observations.

Recent discoveries

In 2004, astronomers found 31 candidate supermassive black holes from searching obscured quasars. The lead scientist said that there are from two to five times as many supermassive black holes as previously predicted.

In June 2004 astronomers found a super-massive black hole, Q0906+6930, at the centre of a distant galaxy about 12.7 billion light years away. This observation indicated rapid creation of super-massive black holes in the early universe.

In November 2004 a team of astronomers reported the discovery of the first intermediate-mass black hole in our Galaxy, orbiting three light-years from Sagittarius A*. This medium black hole of 1,300 solar masses is within a cluster of seven stars, possibly the remnant of a massive star cluster that has been stripped down by the Galactic Centre. This observation may add support to the idea that supermassive black holes grow by absorbing nearby smaller black holes and stars.

In February 2005, a blue giant star SDSS J090745.0+24507 was found to be leaving the Milky Way at twice the escape velocity (0.0022 of the speed of light), having been catapulted out of the galactic core which its path can be traced back to. The high velocity of this star supports the hypothesis of a super-massive black hole in the centre of the galaxy.

The formation of micro black holes on Earth in particle accelerators has been tentatively reported, but not yet confirmed. So far there are no observed candidates for primordial black holes.

Features and theories

Black holes require the general relativistic concept of a curved spacetime: their most striking properties rely on a distortion of the geometry of the space surrounding them.

Gravitational field

The gravitational field outside a black hole is identical to the field produced by any other spherically symmetric object of the same mass. The popular conception of black holes as "sucking" things in is false: objects can orbit around black holes indefinitely without getting any closer. The strange properties of spacetime only become noticeable closer to the black hole.

Event horizon

The "surface" of a black hole is the so-called event horizon, an imaginary surface surrounding the mass of the black hole. Stephen Hawking proved that the topology of the event horizon of a non-spinning black hole is a sphere. At the event horizon, the escape velocity is more than the speed of light. This is why anything inside the event horizon, including a photon, is prevented from escaping across the event horizon by the extremely strong gravitational field. Particles from outside this region can fall in, cross the event horizon, and will never be able to leave.

Since external observers cannot probe the interior of a black hole, according to classical general relativity, black holes can be entirely characterised according to three parameters: mass, angular momentum, and electric charge. This principle is summarised by the saying, coined by John Archibald Wheeler, "black holes have no hair" meaning that there are no features that distinguish one black hole from another, other than mass, charge, and angular momentum.

Space-time distortion and frame of reference

Objects in a gravitational field experience a slowing down of time, called time dilation. This phenomenon has been verified experimentally in the Scout rocket experiment of 1976, and is, for example, taken into account in the Global Positioning System (GPS). Near the event horizon, the time dilation increases rapidly.

From the viewpoint of a distant observer, an object falling into a black hole appears to slow down, approaching but never quite reaching the event horizon. As the object falls into the black hole, it appears redder and dimmer to the distant observer, due to the extreme gravitational red shift caused by the gravity of the black hole. Eventually, the falling object becomes so dim that it can no longer be seen, at a point just before it reaches the event horizon.

From the viewpoint of the falling object, nothing particularly special happens at the event horizon. The object crosses the event horizon and reaches the singularity at the center within a finite amount of proper time, as measured by a watch carried with the falling observer.

From the viewpoint of the falling observer distant objects may appear either blue-shifted or red-shifted, depending on his exact trajectory. Light is blue-shifted by the gravity of the black hole, but is red-shifted by the velocity of the falling object.

Inside the event horizon

Spacetime inside the event horizon of an uncharged non-rotating black hole is peculiar in that the singularity is in every observer's future, so all particles within the event horizon move inexorably towards it (Penrose and Hawking). This means that there is a conceptual inaccuracy in the non-relativistic concept of a black hole as originally proposed by John Michell in 1783. In Michell's theory, the escape velocity equals the speed of light, but it would still, for example, be theoretically possible to hoist an object out of a black hole using a rope. General relativity eliminates such loopholes, because once an object is inside the event horizon, its time-line contains an end-point to time itself, and no possible world-lines come back out through the event horizon. A consequence of this is that a pilot in a powerful rocket ship that had just crossed the event horizon who tried to accelerate away from the singularity would reach it sooner in his frame, since geodesics (unaccelerated paths) are paths that maximise proper time.

As the object continues to approach the singularity, it will be stretched radially with respect to the black hole and compressed in directions perpendicular to this axis. This phenomenon, called spaghettification, occurs as a result of tidal forces: the parts of the object closer to the singularity feel a stronger pull towards it (causing stretching along the axis), and all parts are pulled in the direction of the singularity, which is only aligned with the object's average motion along the axis of the object (causing compression towards the axis).

Singularity

At the center of the black hole, well inside the event horizon, general relativity predicts a singularity, a place where the curvature of spacetime becomes infinite and gravitational forces become infinitely strong.

It is expected that future refinements or generalisations of general relativity (in particular quantum gravity) will change what is thought about the nature of black hole interiors. Most theorists interpret the mathematical singularity of the equations as indicating that the current theory is not complete, and that new phenomena must come into play as one approaches the singularity.

The cosmic censorship hypothesis asserts that there are no naked singularities in general relativity. This hypothesis is that every singularity is hidden behind an event horizon and cannot be probed. Whether this hypothesis is true remains an active area of theoretical research.

Rotating black holes

Main article: rotating black hole

An artist's impression of a black hole with a closely orbiting companion star that exceeds its Roche limit. In-falling matter forms an accretion disk, with some of the matter being ejected in highly energetic polar jets.

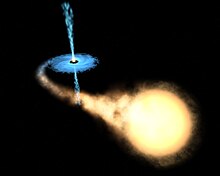
According to theory, the event horizon of a black hole that is not spinning is spherical, and its singularity is expected to be a single point where the curvature becomes infinite. If the black hole carries angular momentum (inherited from a star that is spinning at the time of its collapse), it begins to drag space-time surrounding the event horizon in an effect known as frame-dragging. This spinning area surrounding the event horizon is called the ergosphere and has an ellipsoidal shape. Since the ergosphere is located outside the event horizon, objects can exist within the ergosphere without falling into the hole. However, because space-time itself is moving in the ergosphere, it is impossible for objects to remain in a fixed position. Objects grazing the ergosphere could in some circumstances be catapulted outwards at great speed, extracting energy (and angular momentum) from the hole, hence the Greek name ergosphere ("sphere of work") because it is capable of doing work.

The singularity inside a rotating black hole is expected to be a ring, rather than a point, though the interior geometry of a rotating black hole is currently not well understood. While the fate of an observer falling into a non-rotating black hole is spaghettification, the fate of an observer falling into a rotating black hole is much less clear. For instance, in the Kerr geometry, an infalling observer can potentially escape spaghettification by passing through an inner horizon. However, it is unlikely that the actual interior geometry of a rotating black hole is the Kerr geometry due to stability issues, and the ultimate fate of an observer falling into a rotating black hole is currently not known.

Entropy and Hawking radiation

In 1971, Stephen Hawking showed that the total area of the event horizons of any collection of classical black holes can never decrease. This sounded remarkably similar to the Second Law of Thermodynamics, with area playing the role of entropy. Classically, one could violate the second law of thermodynamics by material entering a black hole disappearing from our universe and resulting in a decrease of the total entropy of the universe. Therefore, Jacob Bekenstein proposed that a black hole should have an entropy and that it should be proportional to its horizon area. Since black holes do not classically emit radiation, the thermodynamic viewpoint was simply an analogy. However, in 1974, Hawking applied quantum field theory to the curved spacetime around the event horizon and discovered that black holes can emit Hawking radiation, a form of thermal radiation. Using the first law of black hole mechanics, it follows that the entropy of a black hole is one quarter of the area of the horizon. This is a universal result and can be extended to apply to cosmological horizons such as in de Sitter space. It was later suggested that black holes are maximum-entropy objects, meaning that the maximum entropy of a region of space is the entropy of the largest black hole that can fit into it. This led to the holographic principle.

The Hawking radiation reflects a characteristic temperature of the black hole, which can be calculated from its entropy. This temperature in fact falls the more massive a black hole becomes: the more energy a black hole absorbs, the colder it gets. A black hole with roughly the mass of the planet Mercury would have a temperature in equilibrium with the cosmic microwave background radiation (about 2.73 K). More massive than this, a black hole will be colder than the background radiation, and it will gain energy from the background faster than it gives energy up through Hawking radiation, becoming even colder still. However, for a less massive black hole the effect implies that the mass of the black hole will slowly evaporate with time, with the black hole becoming hotter and hotter as it does so. Although these effects are negligible for black holes massive enough to have been formed astronomically, they would rapidly become significant for hypothetical smaller black holes, where quantum-mechanical effects dominate. Indeed, small black holes are predicted to undergo runaway evaporation and eventually vanish in a burst of radiation.

Although general relativity can be used to perform a semi-classical calculation of black hole entropy, this situation is theoretically unsatisfying. In statistical mechanics, entropy is understood as counting the number of microscopic configurations of a system which have the same macroscopic qualities(such as mass, charge, pressure, etc.). But without a satisfactory theory of quantum gravity, one cannot perform such a computation for black holes. Some promise has been shown by string theory, however. There one posits that the microscopic degrees of freedom of the black hole are D-branes. By counting the states of D-branes with given charges and energy, the entropy for certain supersymmetric black holes has been reproduced. Extending the region of validity of these calculations is an ongoing area of research.

Black hole unitarity

An open question in fundamental physics is the so-called information loss paradox, or black hole unitarity paradox. Classically, the laws of physics are the same run forward or in reverse. That is, if the position and velocity of every particle in the universe were measured, we could (disregarding chaos) work backwards to discover the history of the universe arbitrarily far in the past. In quantum mechanics, this corresponds to a vital property called unitarity which has to do with the conservation of probability.

Black holes, however, might violate this rule. The position under classical general relativity is subtle but straightforward: because of the classical no hair theorem, we can never determine what went into the black hole. However, as seen from the outside, information is never actually destroyed, as matter falling into the black hole appears from the outside to become more and more red-shifted as it approaches (but never ultimately appears to reach) the event horizon.

Ideas of quantum gravity, on the other hand, suggest that there can only be a limited finite entropy (ie a maximum finite amount of information) associated with the space near the horizon; but the change in the entropy of the horizon plus the entropy of the Hawking radiation is always sufficient to take up all of the entropy of matter and energy falling into the black hole.

Many physicists are concerned however that this is still not sufficiently well understood. In particular, at a quantum level, is the quantum state of the Hawking radiation uniquely determined by the history of what has fallen into the black hole; and is the history of what has fallen into the black hole uniquely determined by the quantum state of the black hole and the radiation? This is what determinism, and unitarity, would require.

For a long time Stephen Hawking had opposed such ideas, holding to his original 1975 position that the Hawking radiation is entirely thermal and therefore entirely random, representing new nondeterministically created information. However, on 21 July 2004 he presented a new argument, reversing his previous position. On this new calculation, the entropy associated with the black hole itself would still be inaccessible to external observers; and in the absence of this information, it is impossible to relate in a 1:1 way the information in the Hawking radiation (embodied in its detailed internal correlations) to the initial state of the system. However, if the black hole evaporates completely, then such an identification can be made, and unitarity is preserved. It is not clear how far even the specialist scientific community is yet persuaded by the mathematical machinery Hawking has used (indeed many regard all work on quantum gravity so far as highly speculative); but Hawking himself found it sufficiently convincing to pay out on a bet he had made in 1997 with Caltech physicist John Preskill, to considerable media interest.

Mathematical theory

Further information: Schwarzschild metric and Deriving the Schwarzschild solution

Black holes are predictions of Albert Einstein's theory of general relativity. There are many known solutions to the Einstein field equations which describe black holes, and they are also thought to be an inevitable part of the evolution of any star of a certain size. In particular, they occur in the Schwarzschild metric, one of the earliest and simplest solutions to Einstein's equations, found by Karl Schwarzschild in 1915. This solution describes the curvature of spacetime in the vicinity of a static and spherically symmetric object, where the metric is,

$ds^{2}=-c^{2}\left(1-{2Gm \over c^{2}r}\right)dt^{2}+\left(1-{2Gm \over c^{2}r}\right)^{-1}dr^{2}+r^{2}d\Omega ^{2}$,

where $d\Omega ^{2}=d\theta ^{2}+\sin ^{2}\theta \;d\phi ^{2}$ is a standard element of solid angle.

According to general relativity, a gravitating object will collapse into a black hole if its radius is smaller than a characteristic distance, known as the Schwarzschild radius. (Indeed, Buchdahl's theorem in general relativity shows that in the case of a perfect fluid model of a compact object, the true lower limit is somewhat larger than the Schwarzschild radius.) Below this radius, spacetime is so strongly curved that any light ray emitted in this region, regardless of the direction in which it is emitted, will travel towards the centre of the system. Because relativity forbids anything from traveling faster than light, anything below the Schwarzschild radius – including the constituent particles of the gravitating object – will collapse into the centre. A gravitational singularity, a region of theoretically infinite density, forms at this point. Because not even light can escape from within the Schwarzschild radius, a classical black hole would truly appear black.

The Schwarzschild radius is given by

$r_{\rm {S}}={2\,Gm \over c^{2}}$

where G is the gravitational constant, m is the mass of the object, and c is the speed of light. For an object with the mass of the Earth, the Schwarzschild radius is a mere 9 millimeters — about the size of a marble.

The mean density inside the Schwarzschild radius decreases as the mass of the black hole increases, so while an earth-mass black hole would have a density of 2 × 10³⁰ kg/m³, a supermassive black hole of 10⁹ solar masses has a density of around 20 kg/m³, less than water! The mean density is given by

$\rho ={\frac {3\,c^{6}}{32\pi m^{2}G^{3}}}$

Since the Earth has a mean radius of 6371 km, its volume would have to be reduced 4 × 10²⁶ times to collapse into a black hole. For an object with the mass of the Sun, the Schwarzschild radius is approximately 3 km, much smaller than the Sun's current radius of about 696,000 km. It is also significantly smaller than the radius to which the Sun will ultimately shrink after exhausting its nuclear fuel, which is several thousand kilometers. More massive stars can collapse into black holes at the end of their lifetimes.

The formula also implies that any object with a given mean density is a black hole if its radius is large enough. The same formula applies for white holes as well. For example, if the visible universe has a mean density equal to the critical density, then it is a white hole, since its singularity is in the past and not in the future as should be for a black hole.

More general black holes are also predicted by other solutions to Einstein's equations, such as the Kerr metric for a rotating black hole, which possesses a ring singularity. Then we have the Reissner-Nordström metric for charged black holes. Last the Kerr-Newman metric is for the case of a charged and rotating black hole.

There is also the Black Hole Entropy formula:

$S={\frac {Akc^{3}}{4\hbar G}}$

Where A is the area of the event horizon of the black hole, $\hbar$ is Dirac's constant (the "reduced Planck constant"), k is the Boltzmann constant, G is the gravitational constant, c is the speed of light and S is the entropy.

A convenient length scale to measure black hole processes is the "gravitational radius", which is equal to

$r_{\rm {G}}={Gm \over c^{2}}$

When expressed in terms of this length scale, many phenomena appear at integer radii. For example, the radius of a Schwarzschild black hole is two gravitational radii and the radius of a maximally rotating Kerr black hole is one gravitational radius. The location of the light circularization radius around a Schwarzschild black hole (where light may orbit the hole in an unstable circular orbit) is $3r_{\rm {G}}$. The location of the marginally stable orbit, thought to be close to the inner edge of an accretion disk, is at $6r_{\rm {G}}$ for a Schwarzschild black hole.

Alternative models

Several alternative models, which behave like a black hole but avoid the singularity, have been proposed. But most researchers judge these concepts artificial, as they are more complicated but do not give near term observable differences from black holes (see Occam's razor). The most prominent alternative theory is the Gravastar.

In March 2005, physicist George Chapline at the Lawrence Livermore National Laboratory in California proposed that black holes do not exist, and that objects currently thought to be black holes are actually dark-energy stars. He draws this conclusion from some quantum mechanical analyses. Although his proposal currently has little support in the physics community, it was widely reported by the media.

Among the alternate models are Magnetospheric eternally collapsing objects, clusters of elementary particles (e.g., boson stars), fermion balls, self-gravitating, degenerate heavy neutrinos and even clusters of very low mass (~0.04 Msolar) black holes.

See also

• AdS black holes
• AdS/CFT
• BKL singularity
• Black hole entropy
• Black hole thermodynamics
• Charged black holes
• Compact stars
• Dark-energy stars
• Holographic principle
• IMBHs
• Laws of black hole mechanics
• Magnetospheric eternally collapsing object
• Micro black holes
• Neutron star
• Primordial black holes
• Q star
• Rotating black holes
• Supermassive black hole
• Schwarzschild metric
• Schwarzschild radius
• Schwarzschild wormholes
• String theory
• Theory of relativity
• Timeline of black hole physics
• White hole
• Wormhole

References

Popular reading

• Hawking, Stephen (1998). A Brief History of Time. Bantam Books, Inc. ISBN 0-553-38016-8.
• Pickover, Clifford (1998). Black Holes: A Traveler's Guide. Wiley, John & Sons, Inc. ISBN 0-471-19704-1.
• Ferguson, Kitty (1991). Black Holes in Space-Time. Watts Franklin. ISBN 0-531-12524-6.
• Thorne, Kip S. (1994). Black Holes and Time Warps. Norton, W. W. & Company, Inc. ISBN 0-393-31276-3.
• Bekenstein, Jacob (2006). Of Gravity, Black Holes and Information. Di Renzo Editore, Roma. ISBN 88-8323-161-9.

University textbooks and monographs

• Wald, Robert M. (1992). Space, Time, and Gravity: The Theory of the Big Bang and Black Holes. University of Chicago Press. ISBN 0-226-87029-4.
• Chandrasekhar, Subrahmanyan (1999). Mathematical Theory of Black Holes. Oxford University Press. ISBN 0-19-850370-9.
• Thorne, Kip S.; Misner, Charles; Wheeler, John (1973). Gravitation. W. H. Freeman and Company. ISBN 0-7167-0344-0.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Carter, B. (1973). Black hole equilibrium states, in Black Holes, eds. DeWitt B. S. and DeWitt C.
• Frolov, V. P. and Novikov, I. D. (1998), Black hole physics.
• Hawking, S. W. and Ellis, G. F. R. (1973), The large-scale structure of space-time, Cambridge University Press.

Research papers

• Hawking, S. W. (July 2005), Information Loss in Black Holes, arxiv:hep-th/0507171. Stephen Hawking's purported solution to the black hole unitarity paradox, first reported at a conference in July 2004.
• Ghez, A.M. et al. Stellar orbits around the Galactic Center black hole, Astrophysics J. 620 (2005). arXiv:astro-ph/0306130 More accurate mass and position for the black hole at the centre of the Milky Way.
• Hughes, S. A. Trust but verify: the case for astrophysical black holes, arXiv:hep-ph/0511217. Lecture notes from 2005 SLAC Summer Institute.

External links

• Black Holes: Gravity's Relentless Pull Award-winning interactive multimedia Web site about the physics and astronomy of black holes from the Space Telescope Science Institute
• FAQ on black holes
• Schwarzschild Geometry on Andrew Hamilton’s website
• Black Hole in Knowledge storage
• Tufts University: Student Project (Great Kid's Section)
• Movie of Black Hole Candidate from Max Planck Institute
• 13 Apr 2006: UT Brownsville Group Simulates Spinning Black-Hole Binaries
• Black Hole Research News on ScienceDaily
• Scientific American Magazine (July 2003 Issue) The Galactic Odd Couple - giant black holes and stellar baby booms
• Scientific American Magazine (May 2005 Issue) Quantum Black Holes
• SPACE.com All About Black Holes News, Features and Interesting Original Videos
• Black holes explained Information about Black Holes at larger-than-life.org