Jump to content

Blake canonical form: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
"in general" is implicit in statements like this; make explicit to avoid misunderstanding
more history
Line 8: Line 8:


==History==
==History==
It was introduced in 1937 by Archie Blake, who called it the "simplified canonical form";<ref name="Blake_1937"/><ref name="Kinsey_1938"/> it was named in honor of Blake by Frank Markham Brown in 1990.<ref name="Brown_2012"/>{{rp|4, 81}}
Archie Blake presented his canonical form at a meeting of the American Mathematical Society in 1932,<ref>Mr. Archie Blake, "Canonical expressions in Boolean algebra", "Abstracts of Papers", ''Bulletin of the American Mathematical Society'', November 1932, p. 805</ref> and in his 1937 dissertation. He called it the "simplified canonical form";<ref name="Blake_1937"/><ref name="Kinsey_1938"/> it was named in honor of Blake by Frank Markham Brown in 1990.<ref name="Brown_2012"/>{{rp|4, 81}}

==Methods for calculation==
==Methods for calculation==
Blake discussed three methods for calculating the canonical form: exhaustion of implicants, iterated [[consensus (boolean algebra)|consensus]], and multiplication. The iterated consensus method was rediscovered<ref name="Brown_2012"/> by Samson and Mills,<ref>{{cite report | url= | author=E.W. Samson and B.E. Mills | title=Circuit minimization: algebra and algorithms for new Boolean canonical expressions | institution=Air Force Cambridge Research Center | type=Technical Report AFCRC TR 54-21 | pages= | date=Apr 1954 }}</ref> [[Willard van Orman Quine|Quine]],<ref>{{cite journal | jstor=2307285 | author=Willard Van Orman Quine | title=A Way to Simplify Truth Functions | journal=The American Mathematical Monthly | volume=62 | number=9 | pages=627&ndash;631 | date=Nov 1955 }}</ref> and Bing.<ref>{{cite journal | url= | author=K. Bing | title=On simplifying propositional formulas | journal=Bull. Amer. Math. Soc. | volume=61 | number= | pages=560 | month= | year=1955 }}</ref><ref>{{cite journal | url= | author=K. Bing | title=On simplifying truth-functional formulas | journal=J. Symbolic Logic | volume=21 | number= | pages=253&ndash;254 | month= | year=1956 }}</ref>
Blake discussed three methods for calculating the canonical form: exhaustion of implicants, iterated [[consensus (boolean algebra)|consensus]], and multiplication. The iterated consensus method was rediscovered<ref name="Brown_2012"/> by Samson and Mills,<ref>{{cite report | url= | author=E.W. Samson and B.E. Mills | title=Circuit minimization: algebra and algorithms for new Boolean canonical expressions | institution=Air Force Cambridge Research Center | type=Technical Report AFCRC TR 54-21 | pages= | date=Apr 1954 }}</ref> [[Willard van Orman Quine|Quine]],<ref>{{cite journal | jstor=2307285 | author=Willard Van Orman Quine | title=A Way to Simplify Truth Functions | journal=The American Mathematical Monthly | volume=62 | number=9 | pages=627&ndash;631 | date=Nov 1955 }}</ref> and Bing.<ref>{{cite journal | url= | author=K. Bing | title=On simplifying propositional formulas | journal=Bull. Amer. Math. Soc. | volume=61 | number= | pages=560 | month= | year=1955 }}</ref><ref>{{cite journal | url= | author=K. Bing | title=On simplifying truth-functional formulas | journal=J. Symbolic Logic | volume=21 | number= | pages=253&ndash;254 | month= | year=1956 }}</ref>

Revision as of 20:43, 1 January 2020

In Boolean logic, a formula for a Boolean function f is in Blake canonical form (BCF),[1] also called the complete sum of prime implicants,[2] the complete sum,[3] or the disjunctive prime form,[4] when it is a disjunction of all the prime implicants of f.[1]

Relation to other forms

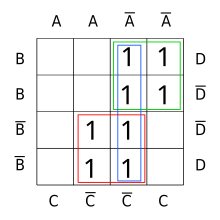
Karnaugh map of AB + BC + AC, a sum of all prime implicants (each rendered in a different color). Deleting AC results in a minimal sum.

The Blake canonical form is a special case of disjunctive normal form.

The Blake canonical form is not necessarily minimal, however all the terms of a minimal sum are contained in the Blake canonical form.[3] On the other hand, the Blake canonical form is unique, whereas there can be multiple minimal forms. Selecting a minimal sum from a Blake canonical form amounts in general to solving the set cover problem,[5] so is NP-hard.[6][7]

History

Archie Blake presented his canonical form at a meeting of the American Mathematical Society in 1932,[8] and in his 1937 dissertation. He called it the "simplified canonical form";[9][10] it was named in honor of Blake by Frank Markham Brown in 1990.[1]: 4, 81 

Methods for calculation

Blake discussed three methods for calculating the canonical form: exhaustion of implicants, iterated consensus, and multiplication. The iterated consensus method was rediscovered[1] by Samson and Mills,[11] Quine,[12] and Bing.[13][14]

See also

References

  1. ^ a b c d Brown, Frank Markham (2012) [2003, 1990]. "Chapter 3: The Blake Canonical Form". Boolean Reasoning - The Logic of Boolean Equations (reissue of 2nd ed.). Mineola, New York: Dover Publications, Inc. pp. 77ff. ISBN 978-0-486-42785-0. [1]
  2. ^ Sasao, Tsutomu (1996). "Ternary Decision Diagrams and their Applications". In Sasao, Tsutomu; Fujita, Masahira (eds.). Representations of Discrete Functions. p. 278. doi:10.1007/978-1-4613-1385-4_12. ISBN 978-0792397205.
  3. ^ a b Kandel, Abraham (1998). Foundations of Digital Logic Design. p. 177. ISBN 9789810231101.
  4. ^ Donald E. Knuth, The Art of Computer Programming 4A: Combinatorial Algorithms, Part 1, 2011, p. 54
  5. ^ Feldman, Vitaly (2009). "Hardness of Approximate Two-Level Logic Minimization and PAC Learning with Membership Queries". Journal of Computer and System Sciences. 75: 13–25 (13–14). doi:10.1016/j.jcss.2008.07.007.
  6. ^ Gimpel, James F. (1965). "A Method for Producing a Boolean Function Having an Arbitrary Prescribed Prime Implicant Table". IEEE Transactions on Computers. 14: 485–488.
  7. ^ Paul, Wolfgang Jakob [in German] (1974). "Boolesche Minimalpolynome und Überdeckungsprobleme". Acta Informatica (in German). 4 (4): 321–336. doi:10.1007/BF00289615.
  8. ^ Mr. Archie Blake, "Canonical expressions in Boolean algebra", "Abstracts of Papers", Bulletin of the American Mathematical Society, November 1932, p. 805
  9. ^ Blake, Archie (1937). Canonical expressions in Boolean algebra (Dissertation). Department of Mathematics, University of Chicago: University of Chicago Libraries.
  10. ^ McKinsey, J. C. C. (June 1938). McKinsey, J. C. C. (ed.). "Blake, Archie. Canonical expressions in Boolean algebra, Department of Mathematics, University of Chicago, 1937". The Journal of Symbolic Logic (Review). 3 (2:93): 93. doi:10.2307/2267634. JSTOR 2267634.
  11. ^ E.W. Samson and B.E. Mills (Apr 1954). Circuit minimization: algebra and algorithms for new Boolean canonical expressions (Technical Report AFCRC TR 54-21). Air Force Cambridge Research Center.
  12. ^ Willard Van Orman Quine (Nov 1955). "A Way to Simplify Truth Functions". The American Mathematical Monthly. 62 (9): 627–631. JSTOR 2307285.
  13. ^ K. Bing (1955). "On simplifying propositional formulas". Bull. Amer. Math. Soc. 61: 560. {{cite journal}}: Cite has empty unknown parameter: |month= (help)
  14. ^ K. Bing (1956). "On simplifying truth-functional formulas". J. Symbolic Logic. 21: 253–254. {{cite journal}}: Cite has empty unknown parameter: |month= (help)
Retrieved from "https://en.wikipedia.org/w/index.php?title=Blake_canonical_form&oldid=933572016"