2-satisfiability: Difference between revisions
m →NL-completeness: characterized by, not characterized as |
→Algorithms: add harv cite to Cook thesis for consistency and to bring out historical order |
||
| Line 47: | Line 47: | ||
| doi = 10.1016/0020-0190(79)90002-4}}.</ref> Since strongly connected components may be found in linear time by an algorithm based on [[depth first search]], the same linear time bound applies as well to 2-satisfiability. |
| doi = 10.1016/0020-0190(79)90002-4}}.</ref> Since strongly connected components may be found in linear time by an algorithm based on [[depth first search]], the same linear time bound applies as well to 2-satisfiability. |
||
It is also possible to solve 2-satisfiability instances in polynomial time using [[first-order resolution]].<ref>{{citation|first=Stephen A.|last=Cook|authorlink=Stephen Cook|contribution=The complexity of theorem-proving procedures|title=Proc. 3rd ACM Symp. Theory of Computing (STOC)|year=1971|pages=151–158|doi=10.1145/800157.805047}}.</ref> Each instance of the resolution rule amounts to finding two implications <math>a\Rightarrow b</math> and <math>b\Rightarrow c</math>, and inferring by [[transitivity]] a third implication <math>a\Rightarrow c</math>. Thus, if one applies this rule until no more implications can be inferred, the resulting collection of implications is described by the [[transitive closure]] of the implication graph, which has polynomial size. The instance is satisfiable if and only if resolution cannot derive an empty clause in the conjunctive normal form of the instance. However, this procedure, while taking only polynomial time, is not as efficient as the linear-time strongly connected component analysis of Aspvall et al. |
It is also possible to solve 2-satisfiability instances in polynomial time using [[first-order resolution]], per {{harvtxt|Cook|1971}}.<ref>{{citation|first=Stephen A.|last=Cook|authorlink=Stephen Cook|contribution=The complexity of theorem-proving procedures|title=Proc. 3rd ACM Symp. Theory of Computing (STOC)|year=1971|pages=151–158|doi=10.1145/800157.805047}}.</ref> Each instance of the resolution rule amounts to finding two implications <math>a\Rightarrow b</math> and <math>b\Rightarrow c</math>, and inferring by [[transitivity]] a third implication <math>a\Rightarrow c</math>. Thus, if one applies this rule until no more implications can be inferred, the resulting collection of implications is described by the [[transitive closure]] of the implication graph, which has polynomial size. The instance is satisfiable if and only if resolution cannot derive an empty clause in the conjunctive normal form of the instance. However, this procedure, while taking only polynomial time, is not as efficient as the linear-time strongly connected component analysis of Aspvall et al. |
||
==Complexity and extensions== |
==Complexity and extensions== |
||
Revision as of 02:11, 20 November 2010
In computer science, 2-satisfiability (abbreviated as 2-SAT or just 2SAT) is the problem of determining whether a collection of two-valued (Boolean or binary) variables with constraints on pairs of variables can be assigned values satisfying all the constraints. In contrast with 3-satisfiability and with constraint satisfaction problems with more than two values per variable, it has a known polynomial time solution. Instances of the 2-satisfiability problem are known as 2-CNF formulas or Krom formulas.
Applications
A number of exact and approximate algorithms for the automatic label placement problem are based on 2-satisfiability. This problem concerns placing textual labels on the features of a diagram or map. Typically, these labels are highly constrained, not only by the map itself (they must be near the feature they label, and not obscure other features), but by each other: two labels will be illegible if they overlap each other. In general, label placement is an NP-hard problem. However, if each feature has only two possible locations for its label (say, extending to the left and to the right of the feature) then it may be solved in polynomial time. For, in this case, one may create a 2-satisfiability instance that has a variable for each label and constraints preventing each pair of labels from being assigned overlapping positions.[1] Similar reductions to 2-satisfiability have been applied to other geometric placement problems including reflection of modules in VLSI designs[2] and edge routing in graph drawing and VLSI layout.[3]
2-satisfiability has also been applied to problems of clustering a set of data points into two clusters minimizing the sum of the cluster diameters,[4] choosing which games in a round-robin tournament schedule to play as home games or away games,[5] recognizing undirected graphs that can be partitioned into an independent set and a small number of complete bipartite subgraphs,[6] inferring business relationships among autonomous subsystems of the internet,[7] reconstruction of evolutionary trees,[8] and digital tomography (reconstructing shapes from cross-sections, as in Nonogram puzzles).[9]
Conjunctive normal form and implicative normal form
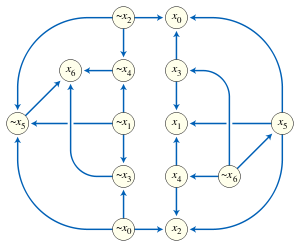
2-SAT instances are normally presented in conjunctive normal form with two variables per clause (2-CNF). That is, the problem is represented as an expression that is a conjunction of disjunctions, where each disjunction has two arguments that may either be variables or the negations of variables. For example, the following formula is in conjunctive normal form, with seven variables and eleven clauses:
As shown above, each variable may occur in multiple clauses of the expression. The 2-satisfiability problem is to find a truth assignment to these variables that makes a formula of this type true. For the expression shown above, one possible satisfying assignment is the one that sets all the variables to true; there are 15 other satisfying assignments as well. Thus, the instance represented by this expression is satisfiable.
The disjunction of any pair of variables is logically equivalent to an implication, in either of two directions:
Therefore, a 2-satisfiability instance may also be written in implicative normal form, in which we replace each disjunction by one of the two implications to which it is equivalent. The implicative normal form of a 2-satisfiability problem can be represented as an implication graph, a skew-symmetric directed graph in which there is one vertex per variable or negated variable, and an edge connecting one vertex to another whenever the corresponding variables are related by an implication in the implicative normal form of the instance.
Algorithms
Unlike 3-satisfiability which is NP-complete and has no known efficient algorithm, 2-satisfiability can be solved in polynomial time. As Krom (1967) observed[10], a 2-satisfiability instance is satisfiable if and only if every variable of the instance belongs to a different strongly connected component of the implication graph than the negation of the same variable. Consequently, 2-SAT instances are commonly referred to as Krom formulas[11]. This was later rediscovered by Aspvall, Plass & Tarjan (1979).[12] Since strongly connected components may be found in linear time by an algorithm based on depth first search, the same linear time bound applies as well to 2-satisfiability.
It is also possible to solve 2-satisfiability instances in polynomial time using first-order resolution, per Cook (1971).[13] Each instance of the resolution rule amounts to finding two implications and , and inferring by transitivity a third implication . Thus, if one applies this rule until no more implications can be inferred, the resulting collection of implications is described by the transitive closure of the implication graph, which has polynomial size. The instance is satisfiable if and only if resolution cannot derive an empty clause in the conjunctive normal form of the instance. However, this procedure, while taking only polynomial time, is not as efficient as the linear-time strongly connected component analysis of Aspvall et al.
Complexity and extensions
NL-completeness
2-satisfiability is NL-complete,[14] meaning that it is one of the "hardest" or "most expressive" problems which can be solved by a nondeterministic Turing machine using only a logarithmic amount of writable memory. The class of problems that can be solved within these space bounds is called NL. These problems can be characterized by second order logic formulas in 2-CNF form; the set of formulas defined in this way is denoted SO(Krom).
A nondeterministic logspace algorithm for determining whether a 2-satisfiability instance is not satisfiable is easy to describe: simply choose (nondeterministically) a variable v and search (nondeterministically) for a chain of implications leading from v to its negation and then back to v. If such a chain is found, the instance cannot be satisfiable. By the Immerman-Szelepcsényi theorem, it is also possible in nondeterministic logspace to verify that a satisfiable 2-SAT instance is satisfiable.
The set of all solutions

The set of all solutions to a 2-satisfiability instance has the structure of a median graph, in which an edge corresponds to the operation of flipping the values of a set of variables that are all constrained to be equal or unequal to each other. In particular, by following edges in this way one can get from any solution to any other solution. Conversely, any median graph can be represented as the set of solutions to a 2-satisfiability instance in this way. The median of any three solutions is formed by setting each variable to the value it holds in the majority of the three solutions; this median always forms another solution to the instance.[15]
Feder (1994) describes an algorithm for efficiently listing all solutions to a given 2-satisfiability instance, and for solving several related problems.[16] There also exist algorithms for finding two satisfying assignments that have the maximal Hamming distance from each other.[17]
Counting the number of satisfying assignments
#2SAT is the problem of counting the number of satisfying assignments to a given 2-CNF formula. This counting problem is #P-complete,[18] which implies that it is not solvable in polynomial time unless P = NP. Moreover, there is no fully polynomial randomized approximation scheme for #2SAT unless NP = RP and this even holds when the input is restricted to monotone 2-CNF formulas, i.e., 2-CNF formulas in which each literal is a positive occurrence of a variable.[19]
The fastest known algorithm for computing the exact number of satisfying assignments to a 2SAT formula runs in time .[20] [21]
Random 2-satisfiability instances
One can form a 2-satisfiability instance at random, for a given number n of variables and m of clauses, by choosing each clause uniformly at random from the set of all possible two-variable clauses. When m is small relative to n, such an instance will likely be satisfiable, but larger values of m have smaller probabilities of being satisfiable. More precisely, if m/n is fixed as a constant α ≠ 1, the probability of satisfiability tends to a limit as n goes to infinity: if α < 1, the limit is one, while if α > 1, the limit is zero. Thus, the problem exhibits a phase transition at α = 1.[22]
Maximum-2-satisfiability
In the maximum-2-satisfiability problem (MAX-2-SAT), the input is a formula in conjunctive normal form with two literals per clause, and the task is to determine the maximum number of clauses that can be simultaneously satisfied by an assignment. MAX-2-SAT is NP-hard and it is a particular case of a maximum satisfiability problem.
By formulating MAX-2-SAT as a problem of finding a cut (that is, a partition of the vertices into two subsets) maximizing the number of edges that have one endpoint in the first subset and one endpoint in the second, in a graph related to the implication graph, and applying semidefinite programming methods to this cut problem, it is possible to find in polynomial time an approximate solution that satisfies at least 0.940... times the optimal number of clauses.[23] A balanced MAX 2-SAT instance is an instance of MAX 2-SAT where every variable appears positively and negatively with equal weight. For this problem, one can improve the approximation ratio to .
Assuming the Unique games conjecture, it is impossible to approximate MAX 2-SAT, balanced or not, with an approximation constant better than 0.943... in polynomial time.[24] Under the weaker assumption that P ≠ NP, the problem is only known to be inapproximable within a constant better than 21/22 = 0.95454...[25]
Various authors have also explored exponential worst-case time bounds for exact solution of MAX-2-SAT instances.[26]
Weighted-2-satisfiability
In the weighted 2-satisfiability problem (W2SAT), the input is an -variable 2SAT instance and an integer , and the problem is to decide whether there exists a satisfying assignment of Hamming weight at most . This problem allows to easily encode the Clique problem and is NP-complete. Moreover, it is a natural W[1]-complete problem,[27] which is a notion from parameterized complexity. It implies that W2SAT is not fixed-parameter tractable unless this holds for all problems in W[1], and thus is unlikely to be computable in time . Moreover, W2SAT cannot be computed in time unless the exponential time hypothesis fails.[28]
References
- ^ Doddi, Srinivas; Marathe, Madhav V.; Mirzaian, Andy; Moret, Bernard M. E.; Zhu, Binhai (1997), "Map labeling and its generalizations", Proc. 8th ACM-SIAM Symp. Discrete Algorithms (SODA), pp. 148–157; Formann, M.; Wagner, F. (1991), "A packing problem with applications to lettering of maps", Proc. 7th ACM Symp. Computational Geometry, pp. 281–288; Poon, Chung Keung; Zhu, Binhai; Chin, Francis (1998), "A polynomial time solution for labeling a rectilinear map", Information Processing Letters, 65 (4): 201–207, doi:10.1016/S0020-0190(98)00002-7; Wagner, Frank; Wolff, Alexander (1997), "A practical map labeling algorithm", Computational Geometry: Theory and Applications, 7 (5–6): 387–404, doi:10.1016/S0925-7721(96)00007-7.
- ^ Boros, Endre; Hammer, Peter L.; Minoux, Michel; Rader, David J., Jr. (1999), "Optimal cell flipping to minimize channel density in VLSI design and pseudo-Boolean optimization", Discrete Applied Mathematics, 90 (1–3): 69–88, doi:10.1016/S0166-218X(98)00114-0
{{citation}}: CS1 maint: multiple names: authors list (link). - ^ Efrat, Alon; Erten, Cesim; Kobourov, Stephen G. (2007), "Fixed-location circular arc drawing of planar graphs" (PDF), Journal of Graph Algorithms and Applications, 11 (1): 145–164; Raghavan, Raghunath; Cohoon, James; Sahni, Sartaj (1986), "Single bend wiring", Journal of Algorithms, 7 (2): 232–237, doi:10.1016/0196-6774(86)90006-4.
- ^ Hansen, P.; Jaumard, B. (1987), "Minimum sum of diameters clustering", Journal of Classification, 4 (2): 215–226, doi:10.1007/BF01896987; Ramnath, Sarnath (2004), "Dynamic digraph connectivity hastens minimum sum-of-diameters clustering", SIAM Journal on Discrete Mathematics, 18 (2): 272–286, doi:10.1137/S0895480102396099.
- ^ Miyashiro, Ryuhei; Matsui, Tomomi (2005), "A polynomial-time algorithm to find an equitable home–away assignment", Operations Research Letters, 33 (3): 235–241, doi:10.1016/j.orl.2004.06.004.
- ^ Brandstädt, Andreas; Hammer, Peter L.; Le, Van Bang; Lozin, Vadim V. (2005), "Bisplit graphs", Discrete Mathematics, 299 (1–3): 11–32, doi:10.1016/j.disc.2004.08.046.
- ^ Wang, Hao; Xie, Haiyong; Yang, Yang Richard; Silberschatz, Avi; Li, Li Erran; Liu, Yanbin (2005), "Stable egress route selection for interdomain traffic engineering: model and analysis", 13th IEEE Conf. Network Protocols (ICNP), pp. 16–29, doi:10.1109/ICNP.2005.39.
- ^ Eskin, Eleazar; Halperin, Eran; Karp, Richard M. (2003), "Efficient reconstruction of haplotype structure via perfect phylogeny", Journal of Bioinformatics and Computational Biology, 1 (1): 1–20, doi:10.1142/S0219720003000174, PMID 15290779.
- ^ Brunetti, Sara; Daurat, Alain (2003), "An algorithm reconstructing convex lattice sets", Theoretical computer science, 304 (1–3): 35–57, doi:10.1016/S0304-3975(03)00050-1; Chrobak, Marek; Dürr, Christoph (1999), "Reconstructing hv-convex polyominoes from orthogonal projections", Information Processing Letters, 69 (6): 283–289, doi:10.1016/S0020-0190(99)00025-3; Kuba, Attila; Balogh, Emese (2002), "Reconstruction of convex 2D discrete sets in polynomial time", Theoretical Computer Science, 283 (1): 223–242, doi:10.1016/S0304-3975(01)00080-9.
- ^ Attention: This template ({{cite doi}}) is deprecated. To cite the publication identified by doi:10.1002/malq.19670130104, please use {{cite journal}} (if it was published in a bona fide academic journal, otherwise {{cite report}} with
|doi=10.1002/malq.19670130104instead.. As cited in Knuth, Donald E. (2009), The Art of Computer Programming, Volume 4, Fascicle 0: Introduction to Combinatorial Algorithms and Boolean Functions, ISBN 0321534964, Theorem K on page 62. preprint of Fascicle 0b (gzip'ed PostScript) available online. - ^ Cook, Stephen; Nguyen, Phuong (2010), Logical Foundations of Proof Complexity, Cambridge University Press
- ^ Aspvall, Bengt; Plass, Michael F.; Tarjan, Robert E. (1979), "A linear-time algorithm for testing the truth of certain quantified boolean formulas" (PDF), Information Processing Letters, 8 (3): 121–123, doi:10.1016/0020-0190(79)90002-4.
- ^ Cook, Stephen A. (1971), "The complexity of theorem-proving procedures", Proc. 3rd ACM Symp. Theory of Computing (STOC), pp. 151–158, doi:10.1145/800157.805047.
- ^ Papadimitriou, Christos H. (1994), Computational Complexity, Addison-Wesley, pp. chapter 4.2, ISBN 0-201-53082-1., Thm. 16.3.
- ^ Bandelt, Hans-Jürgen; Chepoi, Victor (2008), "Metric graph theory and geometry: a survey" (PDF), Contemporary Mathematics, to appear. Chung, F. R. K.; Graham, R. L.; Saks, M. E. (1989), "A dynamic location problem for graphs" (PDF), Combinatorica, 9: 111–132, doi:10.1007/BF02124674. Feder, T. (1995), Stable Networks and Product Graphs, Memoirs of the American Mathematical Society, vol. 555.
- ^ Feder, Tomás (1994), "Network flow and 2-satisfiability", Algorithmica, 11 (3): 291–319, doi:10.1007/BF01240738.
- ^ Angelsmark, Ola; Thapper, Johan (2005), "Algorithms for the maximum Hamming distance problem", Recent Advances in Constraints, Lecture Notes in Computer Science, vol. 3419, Springer-Verlag, pp. 128–141, doi:10.1007/11402763_10.
- ^ Valiant, Leslie G. (1979), "The complexity of enumeration and reliability problems", SIAM Journal on Computing, 8: 410–421, doi:10.1137/0208032
- ^ Welsh, Dominic; Gale, Amy (2001), "The complexity of counting problems", Aspects of complexity: minicourses in algorithmics, complexity and computational algebra: mathematics workshop, Kaikoura, January 7–15, 2000: 115ff, Theorem 57.
- ^ Dahllöf, Vilhelm; Jonsson, Peter; Wahlström, Magnus (2005), "Counting models for 2SAT and 3SAT formulae", Theoretical Computer Science, 332 (1–3): 265–291, doi:10.1016/j.tcs.2004.10.037
- ^ Fürer, Martin; Kasiviswanathan, Shiva Prasad (2007), "Algorithms for counting 2-SAT solutions and colorings with applications", Algorithmic Aspects in Information and Management, Lecture Notes in Computer Science, vol. 4508, Springer-Verlag, pp. 47–57, doi:10.1007/978-3-540-72870-2_5.
- ^ Bollobás, Béla; Borgs, Christian; Chayes, Jennifer T.; Kim, Jeong Han; Wilson, David B. (2001), "The scaling window of the 2-SAT transition", Random Structures and Algorithms, 18 (3): 201–256, doi:10.1002/rsa.1006; Chvátal, V.; Reed, B. (1992), "Mick gets some (the odds are on his side)", Proc. 33rd IEEE Symp. Foundations of Computer Science (FOCS), pp. 620–627, doi:10.1109/SFCS.1992.267789; Goerdt, A. (1996), "A threshold for unsatisfiability", Journal of Computer and System Sciences, 53: 469–486, doi:10.1006/jcss.1996.0081.
- ^ Lewin, Michael; Livnar, Dror; Zwick, Uri (2002), "Improved Rounding Techniques for the MAX 2-SAT and MAX DI-CUT Problems", Proceedings of the 9th International IPCO Conference on Integer Programming and Combinatorial Optimization, Springer-Verlag: 67--82, ISBN 3-540-43676-6
- ^ Khot, Subhash; Kindler, Guy; Mossel, Elchanan; O'Donnell, Ryan (2004), "Optimal Inapproximability Results for MAX-CUT and Other 2-Variable CSPs?", FOCS '04: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, IEEE: 146--154, doi:10.1109/FOCS.2004.49, ISBN 0-7695-2228-9
- ^ Håstad, Johan (2001), "Some optimal inapproximability results", Journal of the Association for Computing Machinery, 48 (4): 798–859, doi:10.1145/502090.502098.
- ^ Bansal, N.; Raman, V. (1999), "Upper bounds for MaxSat: further improved", in Aggarwal, A.; Pandu Rangan, C. (eds.), Proc. 10th Conf. Algorithms and Computation, ISAAC’99, Lecture Notes in Computer Science, vol. 1741, Springer-Verlag, pp. 247–258; Gramm, Jens; Hirsch, Edward A.; Niedermeier, Rolf; Rossmanith, Peter (2003), "Worst-case upper bounds for MAX-2-SAT with an application to MAX-CUT", Discrete Applied Mathematics, 130 (2): 139–155, doi:10.1016/S0166-218X(02)00402-X; Kojevnikov, Arist; Kulikov, Alexander S. (2006), "A new approach to proving upper bounds for MAX-2-SAT", Proc. 17th ACM-SIAM Symp. Discrete Algorithms, pp. 11–17, doi:10.1145/1109557.1109559
- ^ Flum, Jörg; Grohe, Martin (2006), Parameterized Complexity Theory, Springer, ISBN 978-3-540-29952-3
{{citation}}: Invalid|ref=harv(help) - ^ Chen, Jianer; Huang, Xiuzhen; Kanj, Iyad A.; Xia, Ge (2006), "Strong computational lower bounds via parameterized complexity", J. Comput. Syst. Sci., 72 (8): 1346–1367, doi:10.1016/j.jcss.2006.04.007











