Smoothsort: Difference between revisions
Added a very useful web reference |
Update contributor name |
||
| (19 intermediate revisions by 13 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Comparison-based sorting algorithm}} |
|||
{{Infobox Algorithm |
{{Infobox Algorithm |
||
|class=[[Sorting algorithm]] |
|class=[[Sorting algorithm]] |
||
| Line 11: | Line 12: | ||
}} |
}} |
||
In [[computer science]], '''smoothsort''' is a [[comparison sort|comparison-based]] [[sorting algorithm]]. A variant of [[heapsort]], it was invented and published by [[Edsger Dijkstra]] in 1981.<ref name=EWD-796a>{{Cite EWD|796a|16 Aug 1981|Smoothsort – an alternative to sorting in situ|quote=One can also raise the question why I have not chosen as available stretch lengths: ... 63 31 15 7 3 1 which seems attractive since each stretch can then be viewed as the postorder traversal of a balanced binary tree. In addition, the recurrence relation would be simpler. But I know why I chose the Leonardo numbers:}}</ref> Like heapsort, smoothsort is an [[in-place algorithm]] with an upper bound of [[Big O notation|O]](''n'' log ''n''),{{r|hertel}} but it is not a [[stable sort]].<ref>{{cite web |
In [[computer science]], '''smoothsort''' is a [[comparison sort|comparison-based]] [[sorting algorithm]]. A variant of [[heapsort]], it was invented and published by [[Edsger Dijkstra]] in 1981.<ref name=EWD-796a>{{Cite EWD|796a|16 Aug 1981|Smoothsort – an alternative to sorting in situ|quote=One can also raise the question why I have not chosen as available stretch lengths: ... 63 31 15 7 3 1 which seems attractive since each stretch can then be viewed as the postorder traversal of a balanced binary tree. In addition, the recurrence relation would be simpler. But I know why I chose the Leonardo numbers:}}</ref> Like heapsort, smoothsort is an [[in-place algorithm]] with an upper bound of {{math|''[[Big O notation|O]]''(''n'' log ''n'')}} operations (see [[big O notation]]),{{r|hertel}} but it is not a [[stable sort]].<ref>{{cite web |
||
|title=Fastest In-Place Stable Sort |
|||
|first=Craig |last=Brown |
|||
|date=21 Jan 2013 |
|||
|url=http://www.codeproject.com/Articles/26048/Fastest-In-Place-Stable-Sort |
|||
|publisher=[[Code Project]] |
|||
}}{{self-published source|date=January 2016}}</ref>{{self-published inline|date=January 2016}}<ref>{{cite web |
|||
|title=Where is the smoothsort algorithm used? |
|||
|first=David |last=Eisenstat |
|||
|date=13 September 2020 |
|||
|website=Stack Overflow |
|||
|url=https://stackoverflow.com/questions/63872296/where-is-the-smoothsort-algorithm-used/63872426#63872426 |
|||
|access-date=2020-10-28 |
|||
|quote=Smoothsort is not stable, and stability is often more desirable than in-place in practice |
|||
}}</ref> The advantage of smoothsort is that it comes closer to {{math|''O''(''n'')}} time if the [[Adaptive sort|input is already sorted to some degree]], whereas heapsort averages {{math|''O''(''n'' log ''n'')}} regardless of the initial sorted state. |
|||
==Overview== |
==Overview== |
||
Like [[heapsort]], smoothsort organizes the input into a [[priority queue]] and then repeatedly extracts the maximum. Also like heapsort, the priority queue is an [[implicit data structure|implicit]] heap data structure (a [[Heap (data structure)|heap]]-ordered implicit [[binary tree]]), which occupies a prefix of the array. Each extraction shrinks the prefix and adds the extracted element to a growing sorted suffix. When the prefix has shrunk to nothing, the array is completely sorted. |
|||
Like [[heapsort]], smoothsort first transforms the input array into an [[implicit data structure|implicit]] heap data structure, then produces the sorted array by repeatedly extracting the largest remaining element, whose location is determined by the heap structure, and the restoring the structure on the remaining elements. Whereas heapsort uses an implicit tree structure on the array in which a parent node always come before its descendants, so that the initial element is the root of the tree, smoothsort uses an implicit tree structure where a parent node always comes after its descendants. This has some important consequences, such as the fact that not all initial portions of the array correspond to a complete tree; however, it can help to avoid unnecessary displacements as in heapsort, where every element has to pass through the initial position (the root) just before getting swapped to its final position. Indeed, the algorithm is organized so that at the point where an element gets extracted from the heap structure, it is already at the rightmost position among the remaining elements, which is its proper place in the sorted array, so no swap is needed to bring it there. |
|||
Heapsort maps the binary tree to the array using a top-down breadth-first traversal of the tree; the array begins with the root of the tree, then its two children, then four grandchildren, and so on. Every element has a well-defined depth below the root of the tree, and every element except the root has its parent earlier in the array. Its height above the leaves, however, depends on the size of the array. This has the disadvantage that every element must be moved as part of the sorting process: it must pass through the root before being moved to its final location. |
|||
The tree structure defined on array positions is fixed and independent of the array contents. It can be extended to all natural numbers, and doing so there is no root, since every position gets to be a child of a parent further on; however some positions are leaves in an absolute sense. This contrasts with the tree structure used for heapsort, where the initial position is the global root, but there are no absolute leaves, since every position gets two children when sufficiently many positions are added. In the smoothsort structure, every position ''i'' is the root of a unique subtree, whose nodes form an interval that ends at ''i''. An initial interval of positions, and in particular the set of all positions in a given array, might be such an interval corresponding to a subtree, but in general decomposes as a union of a number of successive such subtree intervals, which Dijkstra calls "stretches". Any subtree rooted at a position whose parent lies beyond the initial interval considered gives a stretch in the decomposition of that interval, which decomposition is therefore unique. When a new position following the sequence of stretches is added, one of two things can be the case: either the position is a leaf and adds a stretch of length 1 to the decomposition, or it combines with the last two stretches, becoming the parent of their respective roots, thus replacing the two stretches by a new stretch containing their union plus the new (root) position. |
|||
Smoothsort uses a different mapping, a bottom-up depth-first [[Tree traversal#Post-order, LRN|post-order traversal]]. A left child is followed by the subtree rooted at its sibling, and a right child is followed by its parent. Every element has a well-defined height above the leaves, and every non-leaf element has its ''children'' earlier in the array. Its depth below the root, however, depends on the size of the array. The algorithm is organized so the root is at the end of the heap, and at the moment that an element is extracted from the heap it is already in its final location and does not need to be moved. Also, a sorted array is already a valid heap, and many sorted intervals are valid heap-ordered subtrees. |
|||
Different rules could be used to determine for each position which of the two possibilities applies. For instance, one could stipulate that the last two stretches are combined if and only if they have equal size, in which case all subtrees would be perfect binary trees. Dijkstra's formulation of smoothsort uses a different rule, in which sibling subtrees never have equal sizes (except when both are 1), and the sizes of all subtrees are among a set of values that he calls [[Leonardo numbers]] (they are closely related to [[Fibonacci numbers]]). The general outline of the smoothsort procedure can be defined independently of the rule used to define the implicit tree structure, though the details of its steps depend on that rule. Dijkstra points out<ref name=EWD-796a/> that it would have been possible to use perfect binary trees (of size 2<sup>''k''</sup>−1); this would lead to the same [[Asymptotic analysis|asymptotic efficiency]],{{r|hertel}} but a constant factor in efficiency would be lost due to the on average greater number of stretches that a range of positions breaks up into. |
|||
More formally, every position {{mvar|i}} is the root of a unique subtree, whose nodes occupy a contiguous interval that ends at {{mvar|i}}. An initial prefix of the array (including the whole array), might be such an interval corresponding to a subtree, but in general decomposes as a union of a number of successive such subtree intervals, which Dijkstra calls "stretches". Any subtree without a parent (i.e. rooted at a position whose parent lies beyond the prefix under consideration) gives a stretch in the decomposition of that interval, which decomposition is therefore unique. When a new node is appended to the prefix, one of two cases occurs: either the position is a leaf and adds a stretch of length 1 to the decomposition, or it combines with the last two stretches, becoming the parent of their respective roots, thus replacing the two stretches by a new stretch containing their union plus the new (root) position. |
|||
The rule Dijkstra uses is that the last two stretches are combined if and only if their sizes are ''successive'' Leonardo numbers L(i+1), L(i) (in decreasing order), which numbers are recursively defined as: |
|||
* L(0) = L(1) = 1 |
|||
* L(k+2) = L(k+1) + L(k) + 1 |
|||
As a consequence, the size of any subtree is a Leonardo number. The sequence of sizes stretches decomposing the first ''n'' positions, for any ''n'', can be found in a greedy manner: the first size is the largest Leonardo number not exceeding ''n'', and the remainder (if any) is decomposed recursively. The sizes of stretches are decreasing, strictly so except possibly for two final sizes 1, and avoiding successive Leonardo numbers except possibly for the final two sizes. |
|||
Dijkstra noted{{r|EWD-796a}} that the obvious rule would be to combine stretches if and only if they have equal size, in which case all subtrees would be perfect binary trees of size {{math|2<sup>''k''</sup>−1}}. However, he chose a different rule, which gives more possible tree sizes. This has the same [[Asymptotic analysis|asymptotic efficiency]],{{r|hertel}} but gains a small constant factor in efficiency by requiring fewer stretches to cover each interval. |
|||
In the initial phase of sorting, an increasingly large initial part of the array is reorganized so that the subtree for each of its stretches is a max-heap: the entry at any non-leaf position is at least as large as the entries at the positions that are its children. In addition, the subsequence of root (rightmost) entries of the stretches is kept increasing; this ensures in particular that the final root holds a maximal entry among the interval considered so far. In the second phase one shrinks the interval of interest back to smaller and smaller initial parts of the array, maintaining the same relations as before as the decomposition of the part considered into stretches evolves. At the point where a position disappears from the part under consideration due to shrinking, its entry is maximal among those in the part; as this is true at each shrinking step, those entries are left to sit in their proper position in the sorted result. |
|||
The rule Dijkstra uses is that the last two stretches are combined if and only if their sizes are consecutive [[Leonardo number]]s {{math|''L''(''i''+1)}} and {{math|''L''(''i'')}} (in that order), which numbers are recursively defined, in a manner very similar to the [[Fibonacci number]]s, as: |
|||
The rearrangements necessary to ensure the required relations at all times, and thereby realize the eventual sorting of the array, are as follows. During the first "growing" phase, the heap relation must be enforced whenever two final stretches are combined with a new root to a single stretch; then (also in the case where a singleton stretch was added) the new root has to be compared to any previous roots of stretches to ensure that the subsequence remains increasing, basically by performing an insertion step on the subsequence by repeated swaps with predecessors; and finally, if the new root was moved backwards in this insertion, the max-heap property must be restored for the subtree where it ended (because the entry at the root position has decreased). During the "shrinking" phase, the only worry is keeping the subsequence of roots of stretches increasing as positions are added to and removed from the subsequence. This automatic whenever a stretch of length 1 is removed; however when a longer stretch breaks up and leaves two smaller stretches in its place, the values at their roots are unrelated to the entries at preceding roots, so preserving increase of the subsequence requires two insertion steps, each one (as before) followed by restoring the max-heap property in the stretch where the new entry ends up, unless it remained in its final position. |
|||
* {{math|1=''L''(0) = ''L''(1) = 1}} |
|||
* {{math|1=''L''(''k''+2) = ''L''(''k''+1) + ''L''(''k'') + 1}} |
|||
As a consequence, the size of any subtree is a Leonardo number. The sequence of stretch sizes decomposing the first {{mvar|n}} positions, for any {{mvar|n}}, can be found in a greedy manner: the first size is the largest Leonardo number not exceeding {{mvar|n}}, and the remainder (if any) is decomposed recursively. The sizes of stretches are decreasing, strictly so except possibly for two final sizes 1, and avoiding successive Leonardo numbers except possibly for the final two sizes. |
|||
In addition to each stretch being a heap-ordered tree, the roots of the trees are maintained in sorted order. This effectively adds a third child (which Dijkstra calls a "stepson") to each root linking it to the preceding root. This combines all of the trees together into one global heap. with the global maximum at the end. |
|||
To this general plan, a few refinements are applied to arrive at Dijkstra's sorting procedure. Notably, in the growing phase, ensuring the max-heap property at the root of a newly formed stretch can be combined with ordering it relative to the root of the preceding stretch: if the latter is larger than the new root, then either it also dominates both children of the new root, in which case swapping the roots also repairs the max-heap property, or else swapping the new root with its larger child also repairs the relation with the previous stretch root (but the repair of the max-heap property still needs to propagate down the heap). All in all, at most one series of swaps needs to propagate through the structure during each growing step; by contrast, a shrinking step may as mentioned involve either no such series or two of them. |
|||
Although the location of each node's stepson is fixed, the link only exists for tree roots, meaning that links are removed whenever trees are merged. This is different from ordinary children, which are linked as long as the parent exists. |
|||
Implementation of the implicit tree structures could be easily done by computing once and for all a list of Leonardo numbers and tables for parent and child relations (which do not depend at all on the values to be sorted). But in order to make this qualify as an in-place sorting algorithm, Dijkstra maintains in a slick way a fixed number of integer variables in such a way that at each point in the computation gives access to the relevant information, without requiring any tables. While doing so does not affect complexity, it does take up a large part of the code for the algorithm, and makes the latter more difficult to understand. |
|||
In the first (heap growing) phase of sorting, an increasingly large initial part of the array is reorganized so that the subtree for each of its stretches is a max-heap: the entry at any non-leaf position is at least as large as the entries at the positions that are its children. In addition, all roots are at least as large as their stepsons. |
|||
In the second (heap shrinking) phase, the maximal node is detached from the end of the array (without needing to move it) and the heap invariants are re-established among its children. (Specifically, among the newly created stepsons.) |
|||
Practical implementation frequently needs to compute Leonardo numbers {{math|''L''(''k'')}}. Dijkstra provides clever code which uses a fixed number of integer variables to efficiently compute the values needed at the time they are needed. Alternatively, if there is a finite bound {{mvar|N}} on the size of arrays to be sorted, a precomputed table of Leonardo numbers can be stored in {{math|''O''(log ''N'')}} space. |
|||
==Operations== |
==Operations== |
||
While the two phases of the sorting procedure are opposite to each other as far as the evolution of the sequence-of-heaps structure is concerned, they are implemented using one core primitive, equivalent to the |
|||
"sift down" operation in a binary max-heap. |
|||
===Sifting down=== |
|||
While the two phases of the sorting procedure are opposite to each other as far as the evolution of the sequence-of-heaps structure is concerned, the operations they need to perform to ensure the invariants of the structure have much in common. All these operations are variations of the "sift" operation in a binary max-heap, which restores the heap invariant when it is possibly violated only at the root node. Restoring the increase among the roots of the stretches is obtained by considering the root of each stretch except the first to have as an additional child (Dijkstra uses the term "stepson") the root of the stretch to its left. |
|||
The core sift-down operation (which Dijkstra calls "[[wikt:trinkle|trinkle]]") restores the heap invariant when it is possibly violated only at the root node. If the root node is less than any of its children, it is swapped with its greatest child and the process repeated with the root node in its new subtree. |
|||
The difference between smoothsort and a binary max-heap is that the root of each stretch must be ordered with respect to a third "stepson": the root of the preceding stretch. So the sift-down procedure starts with a series of four-way comparisons (the root node and three children) until the stepson is not the maximal element, then a series of three-way comparisons (the root plus two children) until the root node finds its final home and the invariants are re-established. |
|||
===Growing the heap region by incorporating an element to the right=== |
|||
Each tree is a [[Binary tree#Types of binary trees|full binary tree]]: each node has two children or none. There is no need to deal with the special case of one child which occurs in a standard implicit [[binary heap]]. (But the special case of stepson links more than makes up for this saving.) |
|||
When an additional element is considered for incorporation into the sequence of stretches (list of disjoint heap structures) it either forms a new stretch of its own added to the sequence, or it combines the two rightmost stretches by becoming parent of both their roots and forming a new stretch that replaces the two in the sequence. Which of the two happens depends only on the sizes of the stretches currently present (and ultimately only on the index of the element added); Dijkstra stipulated that stretches are combined if and only if their sizes are {{nowrap|L(k+1)}} and L(k) for some k, i.e., consecutive Leonardo numbers; the new stretch will have size L(k+2). |
|||
Because there are {{math|''O''(log ''n'')}} stretches, each of which is a tree of depth {{math|''O''(log ''n'')}}, the time to perform each sifting-down operation is bounded by {{math|''O''(log ''n'')}}. |
|||
After a new element ''x'' is incorporated into the region of heap structures, as the root of a final stretch that is either a new singleton or obtained by combining two previous stretches, the following procedure called "trinkle" will restore the required relations. The element ''x'' is repeatedly swapped with the root of the previous stretches, as long as this condition holds: there is a stretch immediately to the left of the stretch of ''x'', whose root is greater than ''x'', and ''also'' greater than both of the children of ''x'', if ''x'' has them. Note that at this time no ordering relation between ''x'' and its children has yet been established, and if the largest of its children exceeds ''x'', then it is that child that will become the root once the max-heap property is ensured. After thus moving ''x'' into the appropriate stretch, the heap property of the tree for that stretch is established by "sifting down" the new element to its correct position. This is the same operation as used in heapsort, adapted to the different implicit tree structure used here. It proceeds as follows: while ''x'' is not at a leaf position, and its greater child exceeds ''x'', swap ''x'' with that child and continue sift-down. |
|||
===Growing the heap region by incorporating an element to the right=== |
|||
Because there are {{math|''O''(log ''n'')}} stretches, whose tree structures have depth {{math|''O''(log ''n'')}}, the complexity of trinkle is bounded by {{math|''O''(log ''n'')}}. |
|||
When an additional element is considered for incorporation into the sequence of stretches (list of disjoint heap structures) it either forms a new one-element stretch, or it combines the two rightmost stretches by becoming the parent of both their roots and forming a new stretch that replaces the two in the sequence. Which of the two happens depends only on the sizes of the stretches currently present (and ultimately only on the index of the element added); Dijkstra stipulated that stretches are combined if and only if their sizes are {{math|''L''(''k''+1)}} and {{math|''L''(''k'')}} for some {{mvar|k}}, i.e., consecutive Leonardo numbers; the new stretch will have size {{math|''L''(''k''+2)}}. |
|||
In either case, the new element must be sifted down to its correct place in the heap structure. Even if the new node is a one-element stretch, it must still be sorted relative to the preceding stretch's root. |
|||
The trees used are systematically slightly unbalanced (any left subtree has depth one more than the corresponding right subtree, except when both are singletons); still, the sift-down operation remains somewhat simpler than one that can handle general binary heaps, since each node has either two children or none; there are fewer cases to distinguish. |
|||
====Optimization==== |
====Optimization==== |
||
Dijkstra's algorithm saves work by observing that the full heap invariant is required at the end of the growing phase, but it is not required at every intermediate step. In particular, the requirement that an element be greater than its stepson is only important for the elements which are the final tree roots. |
|||
Therefore, when an element is added, compute the position of its future parent. If this is within the range of remaining values to be sorted, act as if there is no stepson and only sift down within the current tree. |
|||
With respect to the description above, Dijkstra's algorithm implements the following improvement. |
|||
The decision of how to handle the incorporation of a new element is postponed until the type of the next element is inspected: if either that next element is the parent of the current element (having it as right child), or is a leaf but the parent of the current element still is within the range of the array being sorted (when it comes along it will take the current element as left child), then instead of trinkle a simple sift within its subtree is done, avoiding comparison with previous roots. For the final element of the array trinkle is always applied. Thus during the beginning of the growing phase, one is most often just applying sift-down in a single stretch; only those "stepson" relations are considered (by trinkle) that will continue to hold until the end of the growing phase. |
|||
===Shrinking the heap region by separating the rightmost element from it=== |
===Shrinking the heap region by separating the rightmost element from it=== |
||
During this phase, the form of the sequence of stretches goes through the changes of the growing phase in reverse. No work at all is needed when separating off a leaf node, but for a non-leaf node its two children become roots of new stretches, and need to be moved to their proper place in the sequence of roots of stretches. This can be obtained by applying sift-down twice: first for the left child, and then for the right child (whose stepson was the left child). |
|||
Because half of all nodes in a full binary tree are leaves, this performs an average of one sift-down operation per node. |
|||
During this phase, the form of the sequence of stretches goes through the changes of the growing phase in reverse. No work at all is needed when separating off a leaf node, but for a non-leaf node its two children become roots of new stretches, and need to be moved to their proper place in the sequence of roots of stretches. This can be obtained by applying trinkle first for the left child, and then for the right child. |
|||
====Optimization==== |
====Optimization==== |
||
It is already known that the newly exposed roots are correctly ordered with respect to their normal children; it is only the ordering relative to their stepsons which is in question. Therefore, while shrinking the heap, the first step of sifting down can be simplified to a single comparison with the stepson. If a swap occurs, subsequent steps must do the full four-way comparison. |
|||
In this description, one knows that at the position where trinkle starts the heap property is already valid. So I can simplify by, instead of doing the tests that trinkle needs to do, just compare and possibly swap the element with the root before it (if any), and afterwards apply trinkle at its new position if a swap was actually done. Since a swap may invalidate the heap property at the new position where the smaller root moved to, the simplification only applies to the first step. |
|||
==Analysis== |
==Analysis== |
||
Smoothsort takes {{math|''O''(''n'')}} time to process a presorted array |
Smoothsort takes {{math|''O''(''n'')}} time to process a presorted array, {{math|''O''(''n'' log ''n'')}} in the worst case, and achieves nearly linear performance on many nearly sorted inputs. However, it does not handle all nearly sorted sequences optimally. Using the count of inversions as a measure of un-sortedness (the number of pairs of indices {{mvar|i}} and {{mvar|j}} with {{math|''i'' < ''j''}} and {{math|''A''[''i''] > ''A''[''j'']}}; for randomly sorted input this is approximately {{math|''n''<sup>2</sup>/4}}), there are possible input sequences with {{math|''O''(''n'' log ''n'')}} inversions which cause it to take {{math|Ω(''n'' log ''n'')}} time, whereas other [[adaptive sort|adaptive sorting]] algorithms can solve these cases in {{math|''O''(''n'' log log ''n'')}} time.<ref name="hertel">{{cite journal |
||
|last=Hertel |first=Stefan |
|||
|title=Smoothsort's behavior on presorted sequences |
|||
|journal=[[Information Processing Letters]] |
|||
|volume=16 |issue=4 |date=13 May 1983 |pages=165–170 |
|||
|url=http://scidok.sulb.uni-saarland.de/volltexte/2011/4062/pdf/fb14_1982_11.pdf |archive-url=https://web.archive.org/web/20151208051150/http://scidok.sulb.uni-saarland.de/volltexte/2011/4062/pdf/fb14_1982_11.pdf |archive-date=2015-12-08 |url-status=live |
|||
|doi=10.1016/0020-0190(83)90116-3 |
|||
}}</ref> |
|||
The smoothsort algorithm needs to be able to hold in memory the sizes of all of the trees in the Leonardo heap. Since they are sorted by order and all orders are distinct, this is usually done using a [[bit vector]] indicating which orders are present. Moreover, since the largest order is at most {{math|''O''(log |
The smoothsort algorithm needs to be able to hold in memory the sizes of all of the trees in the Leonardo heap. Since they are sorted by order and all orders are distinct, this is usually done using a [[bit vector]] indicating which orders are present. Moreover, since the largest order is at most {{math|''O''(log ''n'')}}, these bits can be encoded in {{math|''O''(1)}} machine words, assuming a [[transdichotomous machine model]]. |
||
Note that {{math|''O''(1)}} machine words is not the same thing as ''one'' machine word. A 32-bit vector would only suffice for sizes less than L(32) = 7049155. A 64-bit vector will do for sizes less than L(64) = 34335360355129 ≈ 2<sup>45</sup>. In general, it takes 1/log<sub>2</sub>(''[[Golden ratio|φ]]'') ≈ 1.44 bits of vector per bit of size. |
Note that {{math|''O''(1)}} machine words is not the same thing as ''one'' machine word. A 32-bit vector would only suffice for sizes less than {{math|1=''L''(32) = 7049155}}. A 64-bit vector will do for sizes less than {{math|1=''L''(64) = 34335360355129 ≈ 2<sup>45</sup>}}. In general, it takes {{math|1/log<sub>2</sub>(''[[Golden ratio|φ]]'') ≈ 1.44}} bits of vector per bit of size. |
||
==Poplar sort== |
|||
A simpler algorithm inspired by smoothsort is '''poplar sort'''.<ref>{{cite journal |
|||
|title=Smoothsort revisited |
|||
|first1=Coenraad |last1=Bron |author-link1=Coenraad Bron |
|||
|first2=Wim H. |last2=Hesselink |
|||
|journal=Information Processing Letters |
|||
|volume=39 |issue=5 |pages=269–276 |date=13 September 1991 |
|||
|doi=10.1016/0020-0190(91)90027-F |
|||
}}</ref> Named after the rows of trees of decreasing size often seen in Dutch [[polder]]s, it performs fewer comparisons than smoothsort for inputs that are not mostly sorted, but cannot achieve linear time for sorted inputs. |
|||
The significant change made by poplar sort in that the roots of the various trees are ''not'' kept in sorted order; there are no "stepson" links tying them together into a single heap. Instead, each time the heap is shrunk in the second phase, the roots are searched to find the maximum entry. |
|||
Because there are {{mvar|n}} shrinking steps, each of which must search {{math|''O''(log ''n'')}} tree roots for the maximum, the best-case run time for poplar sort is {{math|''O''(''n'' log ''n'')}}. |
|||
The authors also suggest using perfect binary trees rather than Leonardo trees to provide further simplification, but this is a less significant change. |
|||
The same structure has been proposed as a general-purpose [[priority queue]] under the name '''post-order heap''',<ref>{{cite conference |
|||
|title=The Post-Order Heap |
|||
|first1=Nicholas J. A. |last1=Harvey |first2=Kevin |last2=Zatloukal |
|||
|url=https://people.csail.mit.edu/nickh/Publications/PostOrderHeap/FUN_abstract.html |
|||
|conference=Third International Conference on Fun with Algorithms (FUN 2004) |
|||
|location=[[Elba]], Italy |date=26–28 May 2004 |
|||
}}</ref> achieving {{math|''O''(1)}} [[Amortized analysis|amortized]] insertion time in a structure simpler than an implicit [[binomial heap]]. |
|||
==Applications== |
|||
The [[musl]] C library uses smoothsort for its implementation of <code>[[qsort]]()</code>.<ref>{{cite web |
|||
|title=How do different languages implement sorting in their standard libraries? |
|||
|url=https://stackoverflow.com/questions/16308374/how-do-different-languages-implement-sorting-in-their-standard-libraries/16309486#16309486 |
|||
|first=Rich |last=Felker |
|||
|date=30 April 2013 |access-date=2020-10-28 |
|||
|website=Stack Overflow |
|||
}}</ref><ref>{{cite web |
|||
|title=src/stdlib/qsort.c |
|||
|first1=Lynn |last1=Ochs |first2=Rich |last2=Felker |
|||
|date=11 August 2017 |access-date=2021-01-26 |
|||
|website=musl - an implementation of the standard library for Linux-based systems |
|||
|url=https://git.musl-libc.org/cgit/musl/tree/src/stdlib/qsort.c |
|||
}}</ref> |
|||
==References== |
==References== |
||
| Line 73: | Line 144: | ||
* [https://www.enterag.ch/hartwig/order/smoothsort.pdf Commented transcription of EWD796a, 16-Aug-1981] |
* [https://www.enterag.ch/hartwig/order/smoothsort.pdf Commented transcription of EWD796a, 16-Aug-1981] |
||
* [https://www.keithschwarz.com/smoothsort/ Detailed modern explanation of Smoothsort] |
* [https://www.keithschwarz.com/smoothsort/ Detailed modern explanation of Smoothsort] |
||
* [[wikibooks:Algorithm Implementation/Sorting/Smoothsort]] |
|||
* [https://github.com/Morwenn/poplar-heap Description and example implementation of Poplar heap] |
|||
{{Edsger Dijkstra}} |
|||
* {{cite journal |
|||
|title=On the Nested Heap Structure in Smoothsort |
|||
|journal={{Nihongo|Mathematical Foundations of Computer Science and Their Applications|数理解析研究所講究録|lead=yes}} |
|||
|last1=Noshita |first1=Kohei |last2=Nakatani |first2=Yoshinobu |
|||
|date=April 1985 |volume=556 |pages=1–16 |hdl=2433/98975 |
|||
|language=en |
|||
|url=http://hdl.handle.net/2433/98975 |
|||
}} |
|||
{{sorting}} |
{{sorting}} |
||
[[Category:Sorting algorithms]] |
|||
[[Category:Comparison sorts]] |
[[Category:Comparison sorts]] |
||
[[Category:Heaps (data structures)]] |
[[Category:Heaps (data structures)]] |
||
Latest revision as of 21:25, 14 October 2024
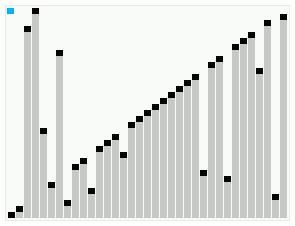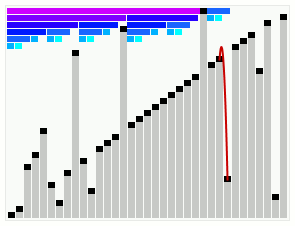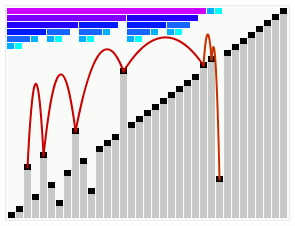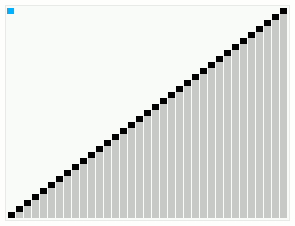 Smoothsort operating on an array which is mostly in order. The bars across the top show the tree structure. | |
| Class | Sorting algorithm |
|---|---|
| Data structure | Array |
| Worst-case performance | O(n log n) |
| Best-case performance | O(n) |
| Average performance | O(n log n) |
| Worst-case space complexity | O(n) total, O(1) auxiliary |
| Optimal | When the data is already sorted |
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981.[1] Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n) operations (see big O notation),[2] but it is not a stable sort.[3][self-published source?][4] The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.
Overview
[edit]Like heapsort, smoothsort organizes the input into a priority queue and then repeatedly extracts the maximum. Also like heapsort, the priority queue is an implicit heap data structure (a heap-ordered implicit binary tree), which occupies a prefix of the array. Each extraction shrinks the prefix and adds the extracted element to a growing sorted suffix. When the prefix has shrunk to nothing, the array is completely sorted.
Heapsort maps the binary tree to the array using a top-down breadth-first traversal of the tree; the array begins with the root of the tree, then its two children, then four grandchildren, and so on. Every element has a well-defined depth below the root of the tree, and every element except the root has its parent earlier in the array. Its height above the leaves, however, depends on the size of the array. This has the disadvantage that every element must be moved as part of the sorting process: it must pass through the root before being moved to its final location.
Smoothsort uses a different mapping, a bottom-up depth-first post-order traversal. A left child is followed by the subtree rooted at its sibling, and a right child is followed by its parent. Every element has a well-defined height above the leaves, and every non-leaf element has its children earlier in the array. Its depth below the root, however, depends on the size of the array. The algorithm is organized so the root is at the end of the heap, and at the moment that an element is extracted from the heap it is already in its final location and does not need to be moved. Also, a sorted array is already a valid heap, and many sorted intervals are valid heap-ordered subtrees.
More formally, every position i is the root of a unique subtree, whose nodes occupy a contiguous interval that ends at i. An initial prefix of the array (including the whole array), might be such an interval corresponding to a subtree, but in general decomposes as a union of a number of successive such subtree intervals, which Dijkstra calls "stretches". Any subtree without a parent (i.e. rooted at a position whose parent lies beyond the prefix under consideration) gives a stretch in the decomposition of that interval, which decomposition is therefore unique. When a new node is appended to the prefix, one of two cases occurs: either the position is a leaf and adds a stretch of length 1 to the decomposition, or it combines with the last two stretches, becoming the parent of their respective roots, thus replacing the two stretches by a new stretch containing their union plus the new (root) position.
Dijkstra noted[1] that the obvious rule would be to combine stretches if and only if they have equal size, in which case all subtrees would be perfect binary trees of size 2k−1. However, he chose a different rule, which gives more possible tree sizes. This has the same asymptotic efficiency,[2] but gains a small constant factor in efficiency by requiring fewer stretches to cover each interval.
The rule Dijkstra uses is that the last two stretches are combined if and only if their sizes are consecutive Leonardo numbers L(i+1) and L(i) (in that order), which numbers are recursively defined, in a manner very similar to the Fibonacci numbers, as:
- L(0) = L(1) = 1
- L(k+2) = L(k+1) + L(k) + 1
As a consequence, the size of any subtree is a Leonardo number. The sequence of stretch sizes decomposing the first n positions, for any n, can be found in a greedy manner: the first size is the largest Leonardo number not exceeding n, and the remainder (if any) is decomposed recursively. The sizes of stretches are decreasing, strictly so except possibly for two final sizes 1, and avoiding successive Leonardo numbers except possibly for the final two sizes.
In addition to each stretch being a heap-ordered tree, the roots of the trees are maintained in sorted order. This effectively adds a third child (which Dijkstra calls a "stepson") to each root linking it to the preceding root. This combines all of the trees together into one global heap. with the global maximum at the end.
Although the location of each node's stepson is fixed, the link only exists for tree roots, meaning that links are removed whenever trees are merged. This is different from ordinary children, which are linked as long as the parent exists.
In the first (heap growing) phase of sorting, an increasingly large initial part of the array is reorganized so that the subtree for each of its stretches is a max-heap: the entry at any non-leaf position is at least as large as the entries at the positions that are its children. In addition, all roots are at least as large as their stepsons.
In the second (heap shrinking) phase, the maximal node is detached from the end of the array (without needing to move it) and the heap invariants are re-established among its children. (Specifically, among the newly created stepsons.)
Practical implementation frequently needs to compute Leonardo numbers L(k). Dijkstra provides clever code which uses a fixed number of integer variables to efficiently compute the values needed at the time they are needed. Alternatively, if there is a finite bound N on the size of arrays to be sorted, a precomputed table of Leonardo numbers can be stored in O(log N) space.
Operations
[edit]While the two phases of the sorting procedure are opposite to each other as far as the evolution of the sequence-of-heaps structure is concerned, they are implemented using one core primitive, equivalent to the "sift down" operation in a binary max-heap.
Sifting down
[edit]The core sift-down operation (which Dijkstra calls "trinkle") restores the heap invariant when it is possibly violated only at the root node. If the root node is less than any of its children, it is swapped with its greatest child and the process repeated with the root node in its new subtree.
The difference between smoothsort and a binary max-heap is that the root of each stretch must be ordered with respect to a third "stepson": the root of the preceding stretch. So the sift-down procedure starts with a series of four-way comparisons (the root node and three children) until the stepson is not the maximal element, then a series of three-way comparisons (the root plus two children) until the root node finds its final home and the invariants are re-established.
Each tree is a full binary tree: each node has two children or none. There is no need to deal with the special case of one child which occurs in a standard implicit binary heap. (But the special case of stepson links more than makes up for this saving.)
Because there are O(log n) stretches, each of which is a tree of depth O(log n), the time to perform each sifting-down operation is bounded by O(log n).
Growing the heap region by incorporating an element to the right
[edit]When an additional element is considered for incorporation into the sequence of stretches (list of disjoint heap structures) it either forms a new one-element stretch, or it combines the two rightmost stretches by becoming the parent of both their roots and forming a new stretch that replaces the two in the sequence. Which of the two happens depends only on the sizes of the stretches currently present (and ultimately only on the index of the element added); Dijkstra stipulated that stretches are combined if and only if their sizes are L(k+1) and L(k) for some k, i.e., consecutive Leonardo numbers; the new stretch will have size L(k+2).
In either case, the new element must be sifted down to its correct place in the heap structure. Even if the new node is a one-element stretch, it must still be sorted relative to the preceding stretch's root.
Optimization
[edit]Dijkstra's algorithm saves work by observing that the full heap invariant is required at the end of the growing phase, but it is not required at every intermediate step. In particular, the requirement that an element be greater than its stepson is only important for the elements which are the final tree roots.
Therefore, when an element is added, compute the position of its future parent. If this is within the range of remaining values to be sorted, act as if there is no stepson and only sift down within the current tree.
Shrinking the heap region by separating the rightmost element from it
[edit]During this phase, the form of the sequence of stretches goes through the changes of the growing phase in reverse. No work at all is needed when separating off a leaf node, but for a non-leaf node its two children become roots of new stretches, and need to be moved to their proper place in the sequence of roots of stretches. This can be obtained by applying sift-down twice: first for the left child, and then for the right child (whose stepson was the left child).
Because half of all nodes in a full binary tree are leaves, this performs an average of one sift-down operation per node.
Optimization
[edit]It is already known that the newly exposed roots are correctly ordered with respect to their normal children; it is only the ordering relative to their stepsons which is in question. Therefore, while shrinking the heap, the first step of sifting down can be simplified to a single comparison with the stepson. If a swap occurs, subsequent steps must do the full four-way comparison.
Analysis
[edit]Smoothsort takes O(n) time to process a presorted array, O(n log n) in the worst case, and achieves nearly linear performance on many nearly sorted inputs. However, it does not handle all nearly sorted sequences optimally. Using the count of inversions as a measure of un-sortedness (the number of pairs of indices i and j with i < j and A[i] > A[j]; for randomly sorted input this is approximately n2/4), there are possible input sequences with O(n log n) inversions which cause it to take Ω(n log n) time, whereas other adaptive sorting algorithms can solve these cases in O(n log log n) time.[2]
The smoothsort algorithm needs to be able to hold in memory the sizes of all of the trees in the Leonardo heap. Since they are sorted by order and all orders are distinct, this is usually done using a bit vector indicating which orders are present. Moreover, since the largest order is at most O(log n), these bits can be encoded in O(1) machine words, assuming a transdichotomous machine model.
Note that O(1) machine words is not the same thing as one machine word. A 32-bit vector would only suffice for sizes less than L(32) = 7049155. A 64-bit vector will do for sizes less than L(64) = 34335360355129 ≈ 245. In general, it takes 1/log2(φ) ≈ 1.44 bits of vector per bit of size.
Poplar sort
[edit]A simpler algorithm inspired by smoothsort is poplar sort.[5] Named after the rows of trees of decreasing size often seen in Dutch polders, it performs fewer comparisons than smoothsort for inputs that are not mostly sorted, but cannot achieve linear time for sorted inputs.
The significant change made by poplar sort in that the roots of the various trees are not kept in sorted order; there are no "stepson" links tying them together into a single heap. Instead, each time the heap is shrunk in the second phase, the roots are searched to find the maximum entry.
Because there are n shrinking steps, each of which must search O(log n) tree roots for the maximum, the best-case run time for poplar sort is O(n log n).
The authors also suggest using perfect binary trees rather than Leonardo trees to provide further simplification, but this is a less significant change.
The same structure has been proposed as a general-purpose priority queue under the name post-order heap,[6] achieving O(1) amortized insertion time in a structure simpler than an implicit binomial heap.
Applications
[edit]The musl C library uses smoothsort for its implementation of qsort().[7][8]
References
[edit]- ^ a b Dijkstra, Edsger W. 16 Aug 1981 (EWD-796a) (PDF). E.W. Dijkstra Archive. Center for American History, University of Texas at Austin.
One can also raise the question why I have not chosen as available stretch lengths: ... 63 31 15 7 3 1 which seems attractive since each stretch can then be viewed as the postorder traversal of a balanced binary tree. In addition, the recurrence relation would be simpler. But I know why I chose the Leonardo numbers:
(transcription) - ^ a b c Hertel, Stefan (13 May 1983). "Smoothsort's behavior on presorted sequences" (PDF). Information Processing Letters. 16 (4): 165–170. doi:10.1016/0020-0190(83)90116-3. Archived (PDF) from the original on 2015-12-08.
- ^ Brown, Craig (21 Jan 2013). "Fastest In-Place Stable Sort". Code Project.[self-published source]
- ^ Eisenstat, David (13 September 2020). "Where is the smoothsort algorithm used?". Stack Overflow. Retrieved 2020-10-28.
Smoothsort is not stable, and stability is often more desirable than in-place in practice
- ^ Bron, Coenraad; Hesselink, Wim H. (13 September 1991). "Smoothsort revisited". Information Processing Letters. 39 (5): 269–276. doi:10.1016/0020-0190(91)90027-F.
- ^ Harvey, Nicholas J. A.; Zatloukal, Kevin (26–28 May 2004). The Post-Order Heap. Third International Conference on Fun with Algorithms (FUN 2004). Elba, Italy.
- ^ Felker, Rich (30 April 2013). "How do different languages implement sorting in their standard libraries?". Stack Overflow. Retrieved 2020-10-28.
- ^ Ochs, Lynn; Felker, Rich (11 August 2017). "src/stdlib/qsort.c". musl - an implementation of the standard library for Linux-based systems. Retrieved 2021-01-26.
External links
[edit]- Commented transcription of EWD796a, 16-Aug-1981
- Detailed modern explanation of Smoothsort
- wikibooks:Algorithm Implementation/Sorting/Smoothsort
- Description and example implementation of Poplar heap
- Noshita, Kohei; Nakatani, Yoshinobu (April 1985). "On the Nested Heap Structure in Smoothsort". Mathematical Foundations of Computer Science and Their Applications (Japanese: 数理解析研究所講究録). 556: 1–16. hdl:2433/98975.
