Isometric projection: Difference between revisions
Fixed apostrophe #article-section-source-editor Tags: Mobile edit Mobile app edit iOS app edit |
|||
| (17 intermediate revisions by 17 users not shown) | |||
| Line 1: | Line 1: | ||
{{Short description|Method for visually representing three-dimensional objects}} |
|||
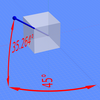
| ⚫ | [[File:3D shapes in isometric projection.svg|thumb|Some 3D shapes |
||
{{Distinguish|Isometry}} |
{{Distinguish|Isometry}} |
||
{{For|isometric projection in video games|isometric video game graphics}} |
{{For|isometric projection in video games|isometric video game graphics}} |
||
| ⚫ | [[File:3D shapes in isometric projection.svg|thumb|Some 3D shapes using the isometric drawing method. The black dimensions are the true lengths as found in an orthographic projection. The red dimensions are used when drawing with the isometric drawing method. The same 3D shapes drawn in isometric projection would appear smaller; an isometric projection will show the object's sides foreshortened, by approximately 80%.]] |
||
{{Views}} |
{{Views}} |
||
'''Isometric projection''' is a method for visually representing three-dimensional objects in two dimensions in [[technical drawing|technical]] and [[engineering drawing]]s. It is an [[axonometric projection]] in which the three [[Cartesian coordinate system|coordinate axes]] appear equally foreshortened and the angle between any two of them is 120 degrees. |
'''Isometric projection''' is a method for visually representing three-dimensional objects in two dimensions in [[technical drawing|technical]] and [[engineering drawing]]s. It is an [[axonometric projection]] in which the three [[Cartesian coordinate system|coordinate axes]] appear equally foreshortened and the angle between any two of them is 120 degrees. |
||
| Line 18: | Line 20: | ||
| footer = |
| footer = |
||
}} |
}} |
||
{{ |
{{comparison of graphical projections.svg|upright}} |
||
The term "isometric" comes from the [[Greek language|Greek]] for "equal measure", reflecting that the [[scale (measurement)|scale]] along each axis of the projection is the same (unlike some other forms of [[graphical projection]]). |
The term "isometric" comes from the [[Greek language|Greek]] for "equal measure", reflecting that the [[scale (measurement)|scale]] along each axis of the projection is the same (unlike some other forms of [[graphical projection]]). |
||
An isometric view of an object can be obtained by choosing the viewing direction such that the angles between the projections of the ''x'', ''y'', and ''z'' [[coordinate axis|axes]] are all the same, or 120°. For example, with a cube, this is done by first looking straight towards one face. Next, the cube is rotated ±45° about the vertical axis, followed by a rotation of approximately 35.264° (precisely arcsin {{frac|1|{{sqrt|3}}}} or arctan {{frac |
An isometric view of an object can be obtained by choosing the viewing direction such that the angles between the projections of the ''x'', ''y'', and ''z'' [[coordinate axis|axes]] are all the same, or 120°. For example, with a cube, this is done by first looking straight towards one face. Next, the cube is rotated ±45° about the vertical axis, followed by a rotation of approximately 35.264° (precisely arcsin {{frac|1|{{sqrt|3}}}} or arctan {{frac|{{sqrt|2}}}}, which is related to the [[Magic angle]]) about the horizontal axis. Note that with the cube (see image) the perimeter of the resulting 2D drawing is a perfect regular hexagon: all the black lines have equal length and all the cube's faces are the same area. Isometric [[graph paper]] can be placed under a normal piece of drawing paper to help achieve the effect without calculation. |
||
In a similar way, an ''isometric view'' can be obtained in a 3D scene. Starting with the camera aligned parallel to the floor and aligned to the coordinate axes, it is first rotated |
In a similar way, an ''isometric view'' can be obtained in a 3D scene. Starting with the camera aligned parallel to the floor and aligned to the coordinate axes, it is first rotated horizontally (around the vertical axis) by ±45°, then 35.264° around the horizontal axis. |
||
Another way isometric projection can be visualized is by considering a view within a cubical room starting in an upper corner and looking towards the opposite, lower corner. The ''x''-axis extends diagonally down and right, the ''y''-axis extends diagonally down and left, and the ''z''-axis is straight up. Depth is also shown by height on the image. Lines drawn along the axes are at 120° to one another. |
Another way isometric projection can be visualized is by considering a view within a cubical room starting in an upper corner and looking towards the opposite, lower corner. The ''x''-axis extends diagonally down and right, the ''y''-axis extends diagonally down and left, and the ''z''-axis is straight up. Depth is also shown by height on the image. Lines drawn along the axes are at 120° to one another. |
||
| Line 29: | Line 31: | ||
In all these cases, as with all [[axonometric projection|axonometric ]] and [[orthographic projections]], such a camera would need a [[Telecentric lens#Object-space telecentric lenses|object-space telecentric lens]], in order that projected lengths not change with distance from the camera. |
In all these cases, as with all [[axonometric projection|axonometric ]] and [[orthographic projections]], such a camera would need a [[Telecentric lens#Object-space telecentric lenses|object-space telecentric lens]], in order that projected lengths not change with distance from the camera. |
||
The term "isometric" is often mistakenly used to refer to axonometric projections, generally. There are, however, actually three types of axonometric projections: ''isometric'', ''[[Dimetric projection|dimetric]]'' and ''[[Oblique projection| |
The term "isometric" is often mistakenly used to refer to axonometric projections, generally. There are, however, actually three types of axonometric projections: ''isometric'', ''[[Dimetric projection|dimetric]]'' and ''[[Oblique projection|oblique]]''. |
||
==Rotation angles== |
==Rotation angles== |
||
From the two angles needed for an isometric projection, the value of the second may seem counterintuitive and deserves some further explanation. |
From the two angles needed for an isometric projection, the value of the second may seem counterintuitive and deserves some further explanation. Let's first imagine a cube with sides of length 2, and its center at the axis origin, which means all its faces intersect the axes at a distance of 1 from the origin. We can calculate the length of the line from its center to the middle of any edge as {{sqrt|2}} using [[Pythagorean theorem|Pythagoras' theorem]] . By rotating the cube by 45° on the ''x''-axis, the point (1, 1, 1) will therefore become (1, 0, {{sqrt|2}}) as depicted in the diagram. The second rotation aims to bring the same point on the positive ''z''-axis and so needs to perform a rotation of value equal to the [[arctangent]] of {{frac|{{sqrt|2}}}} which is approximately 35.264°. |
||
==Mathematics== |
==Mathematics== |
||
There are eight different orientations to obtain an isometric view, depending into which [[octant (solid geometry)|octant]] the viewer looks. The isometric transform from a point ''a''{{sub|''x'',''y'',''z''}} in 3D space to a point ''b''{{sub|''x'',''y''}} in 2D space looking into the first octant can be written mathematically with [[rotation matrix|rotation matrices]] as: |
There are eight different orientations to obtain an isometric view, depending into which [[octant (solid geometry)|octant]] the viewer looks. The isometric transform from a point ''a''{{sub|''x'',''y'',''z''}} in 3D space to a point ''b''{{sub|''x'',''y''}} in 2D space looking into the first octant can be written mathematically with [[rotation matrix|rotation matrices]] as: |
||
<math display="block"> |
|||
\begin{bmatrix} |
\begin{bmatrix} |
||
\mathbf{c}_x \\ |
\mathbf{c}_x \\ |
||
| Line 65: | Line 67: | ||
where ''α'' = arcsin(tan 30°) ≈ 35.264° and ''β'' = 45°. As explained above, this is a rotation around the vertical (here ''y'') axis by ''β'', followed by a rotation around the horizontal (here ''x'') axis by ''α''. This is then followed by an orthographic projection to the ''xy''-plane: |
where ''α'' = arcsin(tan 30°) ≈ 35.264° and ''β'' = 45°. As explained above, this is a rotation around the vertical (here ''y'') axis by ''β'', followed by a rotation around the horizontal (here ''x'') axis by ''α''. This is then followed by an orthographic projection to the ''xy''-plane: |
||
<math display="block"> |
|||
\begin{bmatrix} |
\begin{bmatrix} |
||
\mathbf{b}_x \\ |
\mathbf{b}_x \\ |
||
\mathbf{b}_y \\ |
\mathbf{b}_y \\ |
||
0 \\ |
0 \\ |
||
\end{bmatrix}= |
\end{bmatrix} = |
||
\begin{bmatrix} |
\begin{bmatrix} |
||
1 & 0 & 0 \\ |
1 & 0 & 0 \\ |
||
| Line 89: | Line 91: | ||
|date=December 1978 |
|date=December 1978 |
||
|doi=10.1145/356744.356750 |
|doi=10.1145/356744.356750 |
||
|citeseerx=10.1.1.532.4774 }}</ref> |
|citeseerx=10.1.1.532.4774 |s2cid=708008 }}</ref> |
||
== History and limitations == |
== History and limitations == |
||
| ⚫ | |||
{{multiple image |
{{multiple image |
||
| width = 150 |
| width = 150 |
||
| Line 99: | Line 102: | ||
| caption2 = Example of axonometric art in an illustrated edition of the ''[[Romance of the Three Kingdoms]]'', China, c. 15th century. |
| caption2 = Example of axonometric art in an illustrated edition of the ''[[Romance of the Three Kingdoms]]'', China, c. 15th century. |
||
}} |
}} |
||
| ⚫ | First formalized by Professor [[William Farish (professor)|William Farish]] (1759–1837), the concept of [[isometry]] had existed in a rough empirical form for centuries.<ref>Barclay G. Jones (1986). ''Protecting historic architecture and museum collections from natural disasters''. University of Michigan. {{ISBN|0-409-90035-4}}. p.243.</ref><ref>Charles Edmund Moorhouse (1974). ''Visual messages: graphic communication for senior students''.</ref> From the middle of the 19th century, isometry became an "invaluable tool for engineers, and soon thereafter axonometry and isometry were incorporated in the curriculum of architectural training courses in Europe and the U.S."<ref name="Kri96">J. Krikke (1996). "[http://www.iias.nl/iiasn/iiasn9/eastasia/krikke.html A Chinese perspective for cyberspace?] {{Webarchive| url=https://web.archive.org/web/20160205084728/http://www.iias.nl/iiasn/iiasn9/eastasia/krikke.html |date=2016-02-05 }}". In: ''International Institute for Asian Studies Newsletter'', 9, Summer 1996.</ref> According to Jan Krikke (2000)<ref name="Kri00">Jan Krikke (2000). "Axonometry: a matter of perspective". In: ''Computer Graphics and Applications, IEEE'' Jul/Aug 2000. Vol 20 (4), pp. 7–11.</ref> however, "axonometry originated in China. Its function in Chinese art was similar to [[linear perspective]] in European art. Axonometry, and the pictorial grammar that goes with it, has taken on a new significance with the advent of visual computing".<ref name="Kri00"/> |
||
| ⚫ | |||
| ⚫ | First formalized by Professor [[William Farish (professor)|William Farish]] (1759–1837), the concept of [[isometry]] had existed in a rough empirical form for centuries.<ref>Barclay G. Jones (1986). ''Protecting historic architecture and museum collections from natural disasters''. University of Michigan. {{ISBN|0-409-90035-4}}. p.243.</ref><ref>Charles Edmund Moorhouse (1974). ''Visual messages: graphic communication for senior students''.</ref> From the middle of the 19th century, isometry became an "invaluable tool for engineers, and soon thereafter axonometry and isometry were incorporated in the curriculum of architectural training courses in Europe and the U.S."<ref name="Kri96">J. Krikke (1996). "[http://www.iias.nl/iiasn/iiasn9/eastasia/krikke.html A Chinese perspective for cyberspace?] {{Webarchive|url=https://web.archive.org/web/20160205084728/http://www.iias.nl/iiasn/iiasn9/eastasia/krikke.html |date=2016-02-05 }}". In: ''International Institute for Asian Studies Newsletter'', 9, Summer 1996.</ref> According to Jan Krikke (2000)<ref name="Kri00">Jan Krikke (2000). "Axonometry: a matter of perspective". In: ''Computer Graphics and Applications, IEEE'' Jul/Aug 2000. Vol 20 (4), pp. 7–11.</ref> however, "axonometry originated in |
||
{{multiple image |
{{multiple image |
||
| Line 109: | Line 111: | ||
| caption2 = The [[Penrose stairs]] depicts a staircase which seems to ascend (anticlockwise) or descend (clockwise) yet forms a continuous loop. |
| caption2 = The [[Penrose stairs]] depicts a staircase which seems to ascend (anticlockwise) or descend (clockwise) yet forms a continuous loop. |
||
}} |
}} |
||
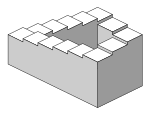
As with all types of [[parallel projection]], objects drawn with isometric projection do not appear larger or smaller as they extend closer to or away from the viewer. While advantageous for [[architectural drawing]]s where measurements need to be taken directly, the result is a perceived distortion, as unlike [[perspective projection]], it is not how [[human vision]] or |
As with all types of [[parallel projection]], objects drawn with isometric projection do not appear larger or smaller as they extend closer to or away from the viewer. While advantageous for [[architectural drawing]]s where measurements need to be taken directly, the result is a perceived distortion, as unlike [[perspective projection]], it is not how [[human vision]] or photography normally work. It also can easily result in situations where depth and altitude are difficult to gauge, as is shown in the illustration to the right or above. This can appear to create paradoxical or [[Impossible object|impossible shapes]], such as the [[Penrose stairs]]. |
||
==Usage in video games and pixel art== |
==Usage in video games and pixel art== |
||
{{main|Isometric video game graphics}} |
{{main|Isometric video game graphics}} |
||
Isometric video game graphics are graphics employed in [[video games]] and [[pixel art]] that utilize a [[parallel projection]], but which angle the [[viewpoint (disambiguation)|viewpoint]] to reveal facets of the environment that would otherwise not be visible from a [[top-down perspective]] or [[Side-scrolling video game|side view]], thereby producing a [[Three-dimensional space|three-dimensional effect]]. Despite the name, isometric computer graphics are not necessarily truly isometric—i.e., the {{mvar|x}}, {{mvar|y}}, and {{mvar|z}} axes are not necessarily oriented 120° to each other. Instead, a variety of angles are used, with [[dimetric projection]] and a 2:1 pixel ratio being the most common. The terms "{{3/4}} perspective", "{{3/4}} view", "[[2.5D]]", and "pseudo 3D" are also sometimes used, although these terms can bear slightly different meanings in other contexts. |
|||
Once common, isometric projection became less so with the advent of more powerful [[3D computer graphics|3D graphics]] systems, and as video games began to focus more on action and individual characters.<ref name="usgamer"/> However, video games utilizing isometric projection—especially [[computer role-playing game]]s—have seen a resurgence in recent years within the [[Indie game|indie gaming]] scene.<ref name="usgamer">{{cite web | url = http://www.usgamer.net/articles/twisted-perspective-the-continued-relevance-of-isometric-games | title = Retronauts: The Continued Relevance of Isometric Games | last = Signor | first = Jeremy | date = 2014-12-19 | website = usgamer.net | publisher = Gamer Network | access-date = 2017-04-01}} |
Once common, isometric projection became less so with the advent of more powerful [[3D computer graphics|3D graphics]] systems, and as video games began to focus more on action and individual characters.<ref name="usgamer"/> However, video games utilizing isometric projection—especially [[computer role-playing game]]s—have seen a resurgence in recent years within the [[Indie game|indie gaming]] scene.<ref name="usgamer">{{cite web | url = http://www.usgamer.net/articles/twisted-perspective-the-continued-relevance-of-isometric-games | title = Retronauts: The Continued Relevance of Isometric Games | last = Signor | first = Jeremy | date = 2014-12-19 | website = usgamer.net | publisher = Gamer Network | access-date = 2017-04-01 |archive-url=https://web.archive.org/web/20220925021110/https://www.usgamer.net/articles/twisted-perspective-the-continued-relevance-of-isometric-games |archive-date=2022-09-25}} |
||
</ref><ref name="bestlooking"> |
</ref><ref name="bestlooking"> |
||
{{cite web |
{{cite web |
||
| Line 124: | Line 126: | ||
| website = kotaku.com | publisher = Gizmodo Media Group |
| website = kotaku.com | publisher = Gizmodo Media Group |
||
| access-date = 2017-04-01 |
| access-date = 2017-04-01 |
||
|archive-url=https://web.archive.org/web/20211010210202/https://kotaku.com/the-best-looking-isometric-games-5991061 |
|||
|archive-date=2021-10-10 |
|||
}} |
}} |
||
</ref> |
</ref> |
||
Latest revision as of 03:47, 14 May 2024

| Part of a series on |
| Graphical projection |
|---|
 |
Isometric projection is a method for visually representing three-dimensional objects in two dimensions in technical and engineering drawings. It is an axonometric projection in which the three coordinate axes appear equally foreshortened and the angle between any two of them is 120 degrees.
Overview
[edit]
The term "isometric" comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (unlike some other forms of graphical projection).
An isometric view of an object can be obtained by choosing the viewing direction such that the angles between the projections of the x, y, and z axes are all the same, or 120°. For example, with a cube, this is done by first looking straight towards one face. Next, the cube is rotated ±45° about the vertical axis, followed by a rotation of approximately 35.264° (precisely arcsin 1⁄√3 or arctan 1⁄√2, which is related to the Magic angle) about the horizontal axis. Note that with the cube (see image) the perimeter of the resulting 2D drawing is a perfect regular hexagon: all the black lines have equal length and all the cube's faces are the same area. Isometric graph paper can be placed under a normal piece of drawing paper to help achieve the effect without calculation.
In a similar way, an isometric view can be obtained in a 3D scene. Starting with the camera aligned parallel to the floor and aligned to the coordinate axes, it is first rotated horizontally (around the vertical axis) by ±45°, then 35.264° around the horizontal axis.
Another way isometric projection can be visualized is by considering a view within a cubical room starting in an upper corner and looking towards the opposite, lower corner. The x-axis extends diagonally down and right, the y-axis extends diagonally down and left, and the z-axis is straight up. Depth is also shown by height on the image. Lines drawn along the axes are at 120° to one another.
In all these cases, as with all axonometric and orthographic projections, such a camera would need a object-space telecentric lens, in order that projected lengths not change with distance from the camera.
The term "isometric" is often mistakenly used to refer to axonometric projections, generally. There are, however, actually three types of axonometric projections: isometric, dimetric and oblique.
Rotation angles
[edit]From the two angles needed for an isometric projection, the value of the second may seem counterintuitive and deserves some further explanation. Let's first imagine a cube with sides of length 2, and its center at the axis origin, which means all its faces intersect the axes at a distance of 1 from the origin. We can calculate the length of the line from its center to the middle of any edge as √2 using Pythagoras' theorem . By rotating the cube by 45° on the x-axis, the point (1, 1, 1) will therefore become (1, 0, √2) as depicted in the diagram. The second rotation aims to bring the same point on the positive z-axis and so needs to perform a rotation of value equal to the arctangent of 1⁄√2 which is approximately 35.264°.
Mathematics
[edit]There are eight different orientations to obtain an isometric view, depending into which octant the viewer looks. The isometric transform from a point ax,y,z in 3D space to a point bx,y in 2D space looking into the first octant can be written mathematically with rotation matrices as:
where α = arcsin(tan 30°) ≈ 35.264° and β = 45°. As explained above, this is a rotation around the vertical (here y) axis by β, followed by a rotation around the horizontal (here x) axis by α. This is then followed by an orthographic projection to the xy-plane:
The other 7 possibilities are obtained by either rotating to the opposite sides or not, and then inverting the view direction or not.[1]
History and limitations
[edit]First formalized by Professor William Farish (1759–1837), the concept of isometry had existed in a rough empirical form for centuries.[3][4] From the middle of the 19th century, isometry became an "invaluable tool for engineers, and soon thereafter axonometry and isometry were incorporated in the curriculum of architectural training courses in Europe and the U.S."[5] According to Jan Krikke (2000)[6] however, "axonometry originated in China. Its function in Chinese art was similar to linear perspective in European art. Axonometry, and the pictorial grammar that goes with it, has taken on a new significance with the advent of visual computing".[6]
As with all types of parallel projection, objects drawn with isometric projection do not appear larger or smaller as they extend closer to or away from the viewer. While advantageous for architectural drawings where measurements need to be taken directly, the result is a perceived distortion, as unlike perspective projection, it is not how human vision or photography normally work. It also can easily result in situations where depth and altitude are difficult to gauge, as is shown in the illustration to the right or above. This can appear to create paradoxical or impossible shapes, such as the Penrose stairs.
Usage in video games and pixel art
[edit]Isometric video game graphics are graphics employed in video games and pixel art that utilize a parallel projection, but which angle the viewpoint to reveal facets of the environment that would otherwise not be visible from a top-down perspective or side view, thereby producing a three-dimensional effect. Despite the name, isometric computer graphics are not necessarily truly isometric—i.e., the x, y, and z axes are not necessarily oriented 120° to each other. Instead, a variety of angles are used, with dimetric projection and a 2:1 pixel ratio being the most common. The terms "3⁄4 perspective", "3⁄4 view", "2.5D", and "pseudo 3D" are also sometimes used, although these terms can bear slightly different meanings in other contexts.
Once common, isometric projection became less so with the advent of more powerful 3D graphics systems, and as video games began to focus more on action and individual characters.[7] However, video games utilizing isometric projection—especially computer role-playing games—have seen a resurgence in recent years within the indie gaming scene.[7][8]
See also
[edit]References
[edit]- ^ Ingrid Carlbom; Joseph Paciorek; Dan Lim (December 1978). "Planar Geometric Projections and Viewing Transformations". ACM Computing Surveys. 10 (4): 465–502. CiteSeerX 10.1.1.532.4774. doi:10.1145/356744.356750. S2CID 708008.
- ^ William Farish (1822) "On Isometrical Perspective". In: Cambridge Philosophical Transactions. 1 (1822).
- ^ Barclay G. Jones (1986). Protecting historic architecture and museum collections from natural disasters. University of Michigan. ISBN 0-409-90035-4. p.243.
- ^ Charles Edmund Moorhouse (1974). Visual messages: graphic communication for senior students.
- ^ J. Krikke (1996). "A Chinese perspective for cyberspace? Archived 2016-02-05 at the Wayback Machine". In: International Institute for Asian Studies Newsletter, 9, Summer 1996.
- ^ a b Jan Krikke (2000). "Axonometry: a matter of perspective". In: Computer Graphics and Applications, IEEE Jul/Aug 2000. Vol 20 (4), pp. 7–11.
- ^ a b Signor, Jeremy (2014-12-19). "Retronauts: The Continued Relevance of Isometric Games". usgamer.net. Gamer Network. Archived from the original on 2022-09-25. Retrieved 2017-04-01.
- ^ Vas, Gergo (2013-03-18). "The Best-Looking Isometric Games". kotaku.com. Gizmodo Media Group. Archived from the original on 2021-10-10. Retrieved 2017-04-01.